搜索
【题目】计算：2sin60°+|3﹣ 
|+（π﹣2）0﹣（ 
）﹣1 ．
参考答案：
【答案】解：原式=2× 
+3﹣ 
+1﹣2=2
【解析】根据特殊角的三角函数值、零指数幂的运算法则、负整数指数幂的运算法则、绝对值的性质进行化简，计算即可．
【考点精析】本题主要考查了零指数幂法则和整数指数幂的运算性质的相关知识点，需要掌握零次幂和负整数指数幂的意义： a0=1（a≠0）;a-p=1/ap（a≠0，p为正整数）；aman=am+n(m、n是正整数)；（am）n=amn(m、n是正整数)；(ab)n=anbn(n是正整数)；am/an=am-n(a不等于0，m、n为正整数）；（a/b）n=an/bn(n为正整数)才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中BC=2，AB=2
，AC=b，且关于x的方程x2﹣4x+b=0有两个相等的实数根，则AC边上的中线长为 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】我国魏晋时期的数学家刘徽创立了“割圆术”，认为圆内接正多边形边数无限增加时，周长就越接近圆周长，由此求得了圆周率π的近似值，设半径为r的圆内接正n边形的周长为L，圆的直径为d，如图所示，当n=6时，π≈
= 
=3，那么当n=12时，π≈ = ． （结果精确到0.01，参考数据：sin15°=cos75°≈0.259） 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，⊙O为等腰△ABC的外接圆，直径AB=12，P为弧
上任意一点（不与B，C重合），直线CP交AB延长线于点Q，⊙O在点P处切线PD交BQ于点D，下列结论正确的是 ． （写出所有正确结论的序号） ①若∠PAB=30°，则弧 
的长为π；②若PD∥BC，则AP平分∠CAB；
③若PB=BD，则PD=6
；④无论点P在弧 上的位置如何变化，CPCQ为定值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】求证：对角线互相垂直的平行四边形是菱形．
小红同学根据题意画出了图形，并写出了已知和求证的一部分，请你补全已知和求证，并写出证明过程．
①已知：如图，在ABCD中，对角线AC，BD交于点O，________．
②求证： -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=x+b与双曲线y=
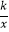（k为常数，k≠0）在第一象限内交于点A（1，2），且与x轴、y轴分别交于B，C两点．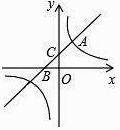 
（1）求直线和双曲线的解析式；
（2）点P在x轴上，且△BCP的面积等于2，求P点的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】为了加强学生课外阅读，开阔视野，某校开展了“书香校园，从我做起”的主题活动，学校随机抽取了部分学生，对他们一周的课外阅读时间进行调查，绘制出频数分布表和频数分布直方图的一部分如下：
课外阅读时间（单位：小时）
频数（人数）
频率
0＜t≤2
2
0.04
2＜t≤4
3
0.06
4＜t≤6
15
0.30
6＜t≤8
a
0.50
t＞8
5
b
请根据图表信息回答下列问题：
（1）频数分布表中的a= ， b=；
（2）将频数分布直方图补充完整；
（3）学校将每周课外阅读时间在8小时以上的学生评为“阅读之星”，请你估计该校2000名学生中评为“阅读之星”的有多少人？
相关试题
