【题目】如图,⊙O为等腰△ABC的外接圆,直径AB=12,P为弧 ![]() 上任意一点(不与B,C重合),直线CP交AB延长线于点Q,⊙O在点P处切线PD交BQ于点D,下列结论正确的是 . (写出所有正确结论的序号) ①若∠PAB=30°,则弧
上任意一点(不与B,C重合),直线CP交AB延长线于点Q,⊙O在点P处切线PD交BQ于点D,下列结论正确的是 . (写出所有正确结论的序号) ①若∠PAB=30°,则弧 ![]() 的长为π;②若PD∥BC,则AP平分∠CAB;
的长为π;②若PD∥BC,则AP平分∠CAB;
③若PB=BD,则PD=6 ![]() ;④无论点P在弧
;④无论点P在弧 ![]() 上的位置如何变化,CPCQ为定值.
上的位置如何变化,CPCQ为定值.
参考答案:
【答案】②③④
【解析】解:如图,连接OP, 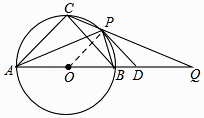
∵AO=OP,∠PAB=30°,
∴∠POB=60°,
∵AB=12,
∴OB=6,
∴弧 ![]() 的长为
的长为 ![]() =2π,故①错误;
=2π,故①错误;
∵PD是⊙O的切线,
∴OP⊥PD,
∵PD∥BC,
∴OP⊥BC,
∴ ![]() =
= ![]() ,
,
∴∠PAC=∠PAB,
∴AP平分∠CAB,故②正确;
若PB=BD,则∠BPD=∠BDP,
∵OP⊥PD,
∴∠BPD+∠BPO=∠BDP+∠BOP,
∴∠BOP=∠BPO,
∴BP=BO=PO=6,即△BOP是等边三角形,
∴PD= ![]() OP=6
OP=6 ![]() ,故③正确;
,故③正确;
∵AC=BC,
∴∠BAC=∠ABC,
又∵∠ABC=∠APC,
∴∠APC=BAC,
又∵∠ACP=∠QCA,
∴△ACP∽△QCA,
∴ ![]() =
= ![]() ,即CPCQ=CA2(定值),故④正确;
,即CPCQ=CA2(定值),故④正确;
所以答案是:②③④.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角),以及对切线的性质定理的理解,了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A在函数y1=﹣
 (x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
(x>0)的图象上,点B在直线y2=kx+1+k(k为常数,且k≥0)上.若A,B两点关于原点对称,则称点A,B为函数y1 , y2图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
A.有1对或2对
B.只有1对
C.只有2对
D.有2对或3对 -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中BC=2,AB=2
 ,AC=b,且关于x的方程x2﹣4x+b=0有两个相等的实数根,则AC边上的中线长为 .
,AC=b,且关于x的方程x2﹣4x+b=0有两个相等的实数根,则AC边上的中线长为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】我国魏晋时期的数学家刘徽创立了“割圆术”,认为圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得了圆周率π的近似值,设半径为r的圆内接正n边形的周长为L,圆的直径为d,如图所示,当n=6时,π≈
 =
=  =3,那么当n=12时,π≈
=3,那么当n=12时,π≈  = . (结果精确到0.01,参考数据:sin15°=cos75°≈0.259)
= . (结果精确到0.01,参考数据:sin15°=cos75°≈0.259) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:2sin60°+|3﹣
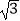 |+(π﹣2)0﹣(
|+(π﹣2)0﹣(  )﹣1 .
)﹣1 . -
科目: 来源: 题型:
查看答案和解析>>【题目】求证:对角线互相垂直的平行四边形是菱形.
小红同学根据题意画出了图形,并写出了已知和求证的一部分,请你补全已知和求证,并写出证明过程.
①已知:如图,在ABCD中,对角线AC,BD交于点O,________.
②求证: -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x+b与双曲线y=
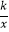 (k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点. 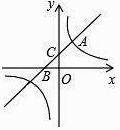
(1)求直线和双曲线的解析式;
(2)点P在x轴上,且△BCP的面积等于2,求P点的坐标.
相关试题

