【题目】如图,在梯形ABCD中,AD∥BC,AB=CD,分别以AB,CD为边向外侧作等边三角形ABE和等边三角形DCF,连接AF,DE. 
(1)求证:AF=DE;
(2)若∠BAD=45°,AB=a,△ABE和△DCF的面积之和等于梯形ABCD的面积,求BC的长.
参考答案:
【答案】
(1)证明:在梯形ABCD中,AD∥BC,AB=CD,
∴∠BAD=∠CDA,
而在等边三角形ABE和等边三角形DCF中,
AB=AE,DC=DF,且∠BAE=∠CDF=60°,
∴AE=DF,∠EAD=∠FDA,AD=DA,
∴△AED≌△DFA(SAS),
∴AF=DE
(2)解:如图作BH⊥AD,CK⊥AD,则有BC=HK,

∵∠BAD=45°,
∴∠HAB=∠KDC=45°,
∴AB= ![]() BH=
BH= ![]() AH,
AH,
同理:CD= ![]() CK=
CK= ![]() KD,
KD,
∵S梯形ABCD= ![]() ,AB=a,
,AB=a,
∴S梯形ABCD= ![]() =
= ![]() ,
,
而S△ABE=S△DCF= ![]() a2,
a2,
∴ ![]() =2×
=2× ![]() a2,
a2,
∴BC= ![]() a.
a.
【解析】(1)根据等腰梯形的性质和等边三角形的性质以及全等三角形的判定方法证明△AED≌△DFA即可;(2)如图作BH⊥AD,CK⊥AD,利用给出的条件和梯形的面积公式即可求出BC的长.
【考点精析】掌握等边三角形的性质和等腰梯形的性质是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°;等腰梯形的两腰相等;同一底上的两个角相等;两条对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)-34+(-8)-5-(-23)
(2)
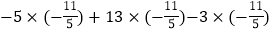
(3)
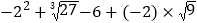
(4)
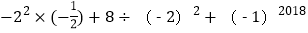
-
科目: 来源: 题型:
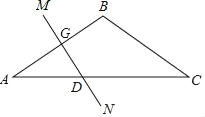
查看答案和解析>>【题目】如图,在△ABC中,BA=BC,∠B=120°,线段AB的垂直平分线MN交AC于点D,且AD=8cm.求:
(1)∠ADG的度数;
(2)线段DC的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一个边长为a的大正方形,剪去一个边长为b的小正方形,即图①称之为“前世”,然后再剪拼成一个新长方形如图②称之为“今生”,请你解答下面的问题:

(1)“前世”图①的面积与“今生”图②新长方形的面积 ;
(2)根据图形面积的和差关系直接写出“前世”图①的面积为: ,标明“今生”图②新长方形的长为 、宽为 ,面积为: .
(3)“形缺数时少直观,数缺形式少形象”它体现了数学的数形结合思想,由(1)和(2)图形面积的计算,形象的验证了代数中的一个乘法公式为: .
(4)请你根据(3)题中乘法公式,计算:2.001×1.999.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知m、x、y满足:(1)
 ;(2)
;(2)  与
与 是同类项.
是同类项. 求代数式
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察算式:
 ;
; ;
; ;
; ;……
;……(1)请根据你发现的规律填空:7×9+1=________2;
(2)用含n的等式表示上面的规律:________;
(3)用找到的规律解决下面的问题:计算:

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系内,反比例函数和二次函数y=k(x2+x﹣1)的图象交于点A(1,k)和点B(﹣1,﹣k).
(1)当k=﹣2时,求反比例函数的解析式;
(2)要使反比例函数和二次函数都是y随着x的增大而增大,求k应满足的条件以及x的取值范围;
(3)设二次函数的图象的顶点为Q,当△ABQ是以AB为斜边的直角三角形时,求k的值.
(4)点C为x轴上一动点,且C点坐标为(2k,0),当△ABC是以AB为斜边的直角三角形时,求K的值.
相关试题

