【题目】如图,把一个边长为a的大正方形,剪去一个边长为b的小正方形,即图①称之为“前世”,然后再剪拼成一个新长方形如图②称之为“今生”,请你解答下面的问题:

(1)“前世”图①的面积与“今生”图②新长方形的面积 ;
(2)根据图形面积的和差关系直接写出“前世”图①的面积为: ,标明“今生”图②新长方形的长为 、宽为 ,面积为: .
(3)“形缺数时少直观,数缺形式少形象”它体现了数学的数形结合思想,由(1)和(2)图形面积的计算,形象的验证了代数中的一个乘法公式为: .
(4)请你根据(3)题中乘法公式,计算:2.001×1.999.
参考答案:
【答案】(1)相等;(2)a2﹣b2,a+b、a﹣b,(a+b)(a﹣b);(3)a2﹣b2=(a+b)(a﹣b);(4)3.999999.
【解析】
(1)根据图形的变化规律即可解决问题;
(2)观察图形即可解决问题;
(3)由(1)(2)可得结论;
(4)利用公式:![]() 即可解决问题;
即可解决问题;
(1)由题意可知:前世”图①的面积与“今生”图②新长方形的面积相等.
故答案为:相等.
(2)根据图形面积的和差关系直接写出“前世”图①的面积为:![]() ,标明“今生”图②新长方形的长为
,标明“今生”图②新长方形的长为![]() 、宽为
、宽为![]() ,面积为:
,面积为:![]() .
.
故答案为:![]() ,
,![]() ,
,![]() ,
,![]() ;
;
(3)“形缺数时少直观,数缺形式少形象”它体现了数学的数形结合思想,由(1)和(2)图形面积的计算,形象的验证了代数中的一个乘法公式为:![]() .
.
故答案为:![]()
(4)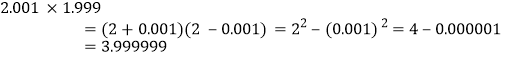 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC三个顶点的坐标分别为A(1,1)、B(4,2)、C(3,4).
(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;
(2)请画出△ABC关于x轴对称的△A2B2C2三个顶点A2、B2、C2的坐标;
(3)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)-34+(-8)-5-(-23)
(2)
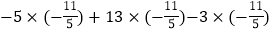
(3)
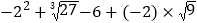
(4)
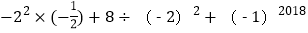
-
科目: 来源: 题型:
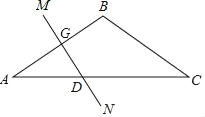
查看答案和解析>>【题目】如图,在△ABC中,BA=BC,∠B=120°,线段AB的垂直平分线MN交AC于点D,且AD=8cm.求:
(1)∠ADG的度数;
(2)线段DC的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,AB=CD,分别以AB,CD为边向外侧作等边三角形ABE和等边三角形DCF,连接AF,DE.

(1)求证:AF=DE;
(2)若∠BAD=45°,AB=a,△ABE和△DCF的面积之和等于梯形ABCD的面积,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知m、x、y满足:(1)
 ;(2)
;(2)  与
与 是同类项.
是同类项. 求代数式
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】观察算式:
 ;
; ;
; ;
; ;……
;……(1)请根据你发现的规律填空:7×9+1=________2;
(2)用含n的等式表示上面的规律:________;
(3)用找到的规律解决下面的问题:计算:

相关试题

