【题目】观察算式:
![]() ;
;![]() ;
;![]() ;
;![]() ;……
;……
(1)请根据你发现的规律填空:7×9+1=________2;
(2)用含n的等式表示上面的规律:________;
(3)用找到的规律解决下面的问题:计算:
![]()
参考答案:
【答案】(1)8;(2)(n-1)×(n+1)+1=n2;(3)![]() .
.
【解析】
(1)由题意得:第一个数字是连续的正整数,第二个数字比第一个数字大2,它们的积加1等于这两数之间的数的平方;
(2)根据(1)中的规律得结论;
(3)首先将括号里进行通分,再将规律代入后约分可得结果.
(1)∵1×3+1=4=22;2×4+1=9=32;3×5+1=16=42;4×6+1=25=52,
∴5×7+1=36=62,6×8+1=49=72,7×9+1=64=82,
故答案为,8;
(2)观察,发现:1×3+1=4=22;2×4+1=9=32;3×5+1=16=42;4×6+1=25=52,…,
∴第n个等式为:n(n+2)+1=(n+1)2,
故答案为:n(n+2)+1=(n+1)2,
(3)![]()
=![]() ×
×![]() ×
×![]() ×…×
×…×![]()
=![]() ×
×![]() ×
×![]() ×…×
×…×![]() ,
,
=2×![]()
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一个边长为a的大正方形,剪去一个边长为b的小正方形,即图①称之为“前世”,然后再剪拼成一个新长方形如图②称之为“今生”,请你解答下面的问题:

(1)“前世”图①的面积与“今生”图②新长方形的面积 ;
(2)根据图形面积的和差关系直接写出“前世”图①的面积为: ,标明“今生”图②新长方形的长为 、宽为 ,面积为: .
(3)“形缺数时少直观,数缺形式少形象”它体现了数学的数形结合思想,由(1)和(2)图形面积的计算,形象的验证了代数中的一个乘法公式为: .
(4)请你根据(3)题中乘法公式,计算:2.001×1.999.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,AB=CD,分别以AB,CD为边向外侧作等边三角形ABE和等边三角形DCF,连接AF,DE.

(1)求证:AF=DE;
(2)若∠BAD=45°,AB=a,△ABE和△DCF的面积之和等于梯形ABCD的面积,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知m、x、y满足:(1)
 ;(2)
;(2)  与
与 是同类项.
是同类项. 求代数式
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系内,反比例函数和二次函数y=k(x2+x﹣1)的图象交于点A(1,k)和点B(﹣1,﹣k).
(1)当k=﹣2时,求反比例函数的解析式;
(2)要使反比例函数和二次函数都是y随着x的增大而增大,求k应满足的条件以及x的取值范围;
(3)设二次函数的图象的顶点为Q,当△ABQ是以AB为斜边的直角三角形时,求k的值.
(4)点C为x轴上一动点,且C点坐标为(2k,0),当△ABC是以AB为斜边的直角三角形时,求K的值. -
科目: 来源: 题型:
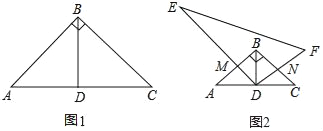
查看答案和解析>>【题目】特例探究:如图①,已知在△ABC中,AB=BC,∠ABC=90°,D为AC边的中点,连接BD,判断△ABD是什么三角形,并说明理由.
归纳证明:如图②,已知在△ABC中,AB=BC,∠ABC=90°,D为AC边的中点,连接BD,把Rt△DEF的直角顶点D放在AC的中点上,DE交AB于M,DF交BC于N.证明:DM=DN.
拓展应用:在图②,AC=4,其他条件都不发生变化,请直接写出Rt△DEF与△ABC的重叠部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AE切⊙O于点E,AT交⊙O于点M,N,线段OE交AT于点C,OB⊥AT于点B,已知∠EAT=30°,AE=3
 ,MN=2
,MN=2  .
.
(1)求∠COB的度数;
(2)求⊙O的半径R;
(3)点F在⊙O上( 是劣弧),且EF=5,把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合.在EF的同一侧,这样的三角形共有多少个?你能在其中找出另一个顶点在⊙O上的三角形吗?请在图中画出这个三角形,并求出这个三角形与△OBC的周长之比.
是劣弧),且EF=5,把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合.在EF的同一侧,这样的三角形共有多少个?你能在其中找出另一个顶点在⊙O上的三角形吗?请在图中画出这个三角形,并求出这个三角形与△OBC的周长之比.
相关试题

