搜索
【题目】如图，在四边型ABCD中，AB∥DC，过对角线AC的中点O作
，分别交边AB,CD于点E,F，连接CE,AF.
（1）求证：四边形AECF是菱形；
（2）若EF=8，AE=5，求四边形AECF的面积.
参考答案：
【答案】（1）见解析；（2）S四边形AECF =24.
【解析】
（1）运用“对角线互相垂直平分的四边形是菱形”判定，已知EF⊥AC，AO=OC，只需要证明OE=OF即可，可用全等三角形得出；
（2）由已知条件，利用勾股定理可求得AO的长度，进而求得AC的长，根据菱形的面积等于对角线乘积的一半即可求解．
解：（1）证明：
∵AB∥CD
∴∠DCA=∠CAB, ∠CFE=∠FEA,
∵AO=OC
∴FOC≌EOA
∴OF=OE
∴四边形
是平行四边形
∵
∴四边形是菱形
（2）∵四边形是平行四边形, EF=8
∴OF=OE=4
由勾股定理，得：
∴AC=2AO=6
∴S四边形AECF= 
=24
-
科目： 来源： 题型：
查看答案和解析>>【题目】△ABC中,∠C=60°，点D，E分别是边AC，BC上的点，点P是直线AB上一动点，连接PD，PE，设∠DPE=α.
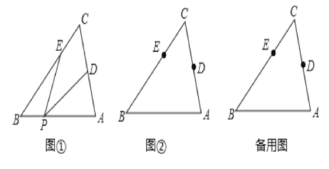
(1)如图①所示,如果点P在线段BA上,且α=30°，那么∠PEB+∠PDA=___；
(2)如图②所示，如果点P在线段BA上运动，
①依据题意补全图形；
②写出∠PEB+∠PDA的大小(用含α的式子表示)；并说明理由。
(3)如果点P在线段BA的延长线上运动,直接写出∠PEB与∠PDA之间的数量关系(用含α的式子表示).那么∠PEB与∠PDA之间的数量关系是___.
-
科目： 来源： 题型：
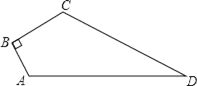
查看答案和解析>>【题目】如图，已知四边形ABCD中，∠B＝90°，AB＝3，BC＝4，CD＝12，AD＝13，求四边形ABCD的面积．
-
科目： 来源： 题型：
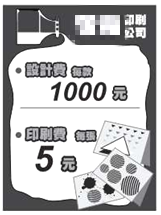
查看答案和解析>>【题目】如图的宣传单为某印刷公司设计与印刷卡片计价方式的说明，小娜打算请此印刷公司设计一款母亲节卡片并印刷，她再将卡片以每张15元的价格贩售.若利润等于收入扣掉成本，且成本只考虑设计费与印刷费，则她至少需印多少张卡片，才可使得卡片全数售出后的利润超过成本的20%？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在□ABCD中，BC=2AB，M是AD的中点，CE⊥AB，垂足为E，求证：∠DME=3∠AEM.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，△ABC三个顶点分别是A（2，0）、B（0，4）、C（-3，0），把△ABC沿x轴向右平移4个单位，得到△A1B1C1．
（1）在图中以黑点为原点建立平面直角坐标系，画出△ABC和△A1B1C1；
（2）写出A1、B1、C1各点的坐标；
（3）求△ABC的面积．
-
科目： 来源： 题型：
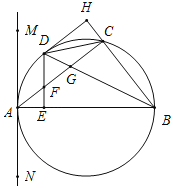
查看答案和解析>>【题目】如图，△ABC内接于半圆，AB是直径，过A作直线MN，∠MAC=∠ABC，D是弧AC的中点，连接BD交AC于G，过D作DE⊥AB于E，交AC于F．
（1）求证：MN是半圆的切线；
（2）作DH⊥BC交BC的延长线于点H，连接CD，试判断线段AE与线段CH的数量关系，并说明理由．
（3）若BC=4，AB=6，试求AE的长．
相关试题
