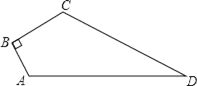
【题目】如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
参考答案:
【答案】36
【解析】
连接AC,由题意可得三角形ABC为直角三角形,由AB与BC的长,利用勾股定理求出AC的长,再由AC,DC及AD的长,利用勾股定理的逆定理得到三角形ADC为直角三角形,分别求出两直角三角形的面积,相加即可得到四边形ABCD的面积.
解:连接AC,

∵∠B=90°,
∴△ABC为直角三角形,
∵BC=4cm,AB=3cm,
∴根据勾股定理得:BD=![]() cm,
cm,
在△ADC中,AC2+DC2=52+122=25+144=169,AD2=132=169,
∵AC2+CD2=AD2,
∴△ACD为直角三角形,
则S四边形ABCD=S△ABC+S△DAC=![]() ABBC+
ABBC+![]() ACCD=
ACCD=![]() ×3×4+
×3×4+![]() ×5×12=6+30=36(cm2).
×5×12=6+30=36(cm2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校在暑假期间开展“心怀感恩,孝敬父母”的实践活动,倡导学生在假期中帮助父母干家务,开学以后,校学生会随机抽取了部分学生,就暑假“平均每天帮助父母干家务所用时长”进行了调查,以下是根据相关数据绘制的统计图的部分:

根据上述信息,回答下列问题:
 在本次随机抽取的样本中,调查的学生人数是 人;
在本次随机抽取的样本中,调查的学生人数是 人;
 ,
, ;
; 补全频数分布直方图;
补全频数分布直方图; 如果该校共有学生
如果该校共有学生 人,请你估计“平均每天帮助父母干家务的时长不少于
人,请你估计“平均每天帮助父母干家务的时长不少于 分钟”的学生大约有多少人?
分钟”的学生大约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个篮球和足球(每个篮球的价格相同,每个足球的价格相同).若购买
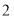 个篮球和
个篮球和 个足球共需
个足球共需 元,购买
元,购买 个篮球和
个篮球和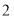 个足球共需
个足球共需 元.
元. 求篮球、足球的单价各是多少元;
求篮球、足球的单价各是多少元; 根据学校实际需要,需一次性购买篮球和足球共
根据学校实际需要,需一次性购买篮球和足球共 个.要求购买篮球和足球的总费用不超过
个.要求购买篮球和足球的总费用不超过 元,则该校最多可以购买多少个篮球?
元,则该校最多可以购买多少个篮球? -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,∠C=60°,点D,E分别是边AC,BC上的点,点P是直线AB上一动点,连接PD,PE,设∠DPE=α.
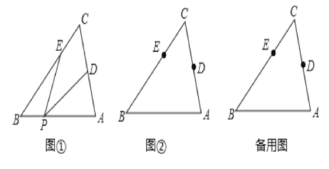
(1)如图①所示,如果点P在线段BA上,且α=30°,那么∠PEB+∠PDA=___;
(2)如图②所示,如果点P在线段BA上运动,
①依据题意补全图形;
②写出∠PEB+∠PDA的大小(用含α的式子表示);并说明理由。
(3)如果点P在线段BA的延长线上运动,直接写出∠PEB与∠PDA之间的数量关系(用含α的式子表示).那么∠PEB与∠PDA之间的数量关系是___.
-
科目: 来源: 题型:
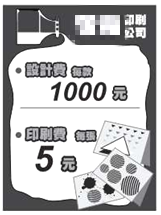
查看答案和解析>>【题目】如图的宣传单为某印刷公司设计与印刷卡片计价方式的说明,小娜打算请此印刷公司设计一款母亲节卡片并印刷,她再将卡片以每张15元的价格贩售.若利润等于收入扣掉成本,且成本只考虑设计费与印刷费,则她至少需印多少张卡片,才可使得卡片全数售出后的利润超过成本的20%?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边型ABCD中,AB∥DC,过对角线AC的中点O作
 ,分别交边AB,CD于点E,F,连接CE,AF.
,分别交边AB,CD于点E,F,连接CE,AF.
(1)求证:四边形AECF是菱形;
(2)若EF=8,AE=5,求四边形AECF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,BC=2AB,M是AD的中点,CE⊥AB,垂足为E,求证:∠DME=3∠AEM.

相关试题

