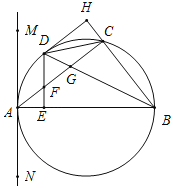
【题目】如图,△ABC内接于半圆,AB是直径,过A作直线MN,∠MAC=∠ABC,D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F.
(1)求证:MN是半圆的切线;
(2)作DH⊥BC交BC的延长线于点H,连接CD,试判断线段AE与线段CH的数量关系,并说明理由.
(3)若BC=4,AB=6,试求AE的长.
参考答案:
【答案】(1)证明见解析;(2)AE=CH,理由见解析;(3)AE=1.
【解析】试题分析:(1)由AB是直径得出∠ACB=90°,推出∠CAB+∠MAC=90°即可;
(2)连接AD,证明△ADE≌△CDH即可;
(3)由(2)可得出AE=CH,且DE=DH,可证得BE=BH,结合BC和AB的长可求出AE.
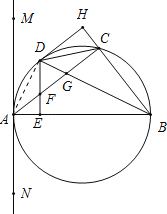
试题解析:(1)如图所示,
∵AB是直径,∴∠ACB=90°,∴∠CAB+∠ABC=90°,
∵∠MAC=∠ABC,∴∠CAB+∠MAC=90°,
即∠MAB=90°,
∴MN是半圆的切线;
(2)AE=CH,理由如下:
连接AD,
∵D是![]() 的中点,∴AD=CD,∠HBD=∠ABD,
的中点,∴AD=CD,∠HBD=∠ABD,
∵DE⊥AB,DH⊥BC,∴DE=DH,且∠AED=∠DHC,
在Rt△ADE和Rt△CDH中,![]() ,∴Rt△ADE≌Rt△CDH(HL),
,∴Rt△ADE≌Rt△CDH(HL),
∴AE=CH;
(3)由(2)知DH=DE,∠DHB=∠DEB=90°,
在△RtDBH和Rt△DBE中,![]() ,∴△RtDBH≌Rt△DBE(HL),
,∴△RtDBH≌Rt△DBE(HL),
∴BE=BH,∴BA﹣AE=BC+CH,且AE=CH,∴BA﹣AE=BC+AE,
又∵AB=6,BC=4,∴6﹣AE=4+AE,
∴AE=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边型ABCD中,AB∥DC,过对角线AC的中点O作
 ,分别交边AB,CD于点E,F,连接CE,AF.
,分别交边AB,CD于点E,F,连接CE,AF.
(1)求证:四边形AECF是菱形;
(2)若EF=8,AE=5,求四边形AECF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,BC=2AB,M是AD的中点,CE⊥AB,垂足为E,求证:∠DME=3∠AEM.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC三个顶点分别是A(2,0)、B(0,4)、C(-3,0),把△ABC沿x轴向右平移4个单位,得到△A1B1C1.
(1)在图中以黑点为原点建立平面直角坐标系,画出△ABC和△A1B1C1;
(2)写出A1、B1、C1各点的坐标;
(3)求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场在春节期间搞优惠促销活动,商场将29英寸和25英寸彩电共96台分别以8折和7折出售,共得168400元。已知29英寸彩电原价为3000元/台,25英寸彩电原价为2000元/台,出售29英寸和25英寸彩电各多少台?
-
科目: 来源: 题型:
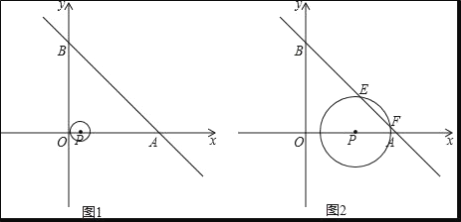
查看答案和解析>>【题目】如图1,一次函数y=﹣x+10的图象交x轴于点A,交y轴于点B.以P(1,0)为圆心的⊙P与y轴相切,若点P以每秒2个单位的速度沿x轴向右平移,同时⊙P的半径以每秒增加1个单位的速度不断变大,设运动时间为t(s)
(1)点A的坐标为 ,点B的坐标为 ,∠OAB= °;
(2)在运动过程中,点P的坐标为 ,⊙P的半径为 (用含t的代数式表示);
(3)当⊙P与直线AB相交于点E、F时
①如图2,求t=
 时,弦EF的长;
时,弦EF的长;②在运动过程中,是否存在以点P为直角顶点的Rt△PEF,若存在,请求出t的值;若不存在,请说明理由(利用图1解题).
-
科目: 来源: 题型:
查看答案和解析>>【题目】学习了统计知识后,数学老师请数学兴趣小组的同学就本班同学的上学方式进行了一次调查统计.如图甲乙是数学兴趣小组的同学们通过手机和整理数据后,绘制的两幅不完整的统计图.
请你根据图中提供的信息,解答一下的问题:
(1)在扇形统计图中,计算出“步行”部分所应对的圆心角的度数.
(2)请问该班共有多少名学生?
(3)在图中将表示“乘车”的部分补充完整.


相关试题

