【题目】△ABC中,∠C=60°,点D,E分别是边AC,BC上的点,点P是直线AB上一动点,连接PD,PE,设∠DPE=α.
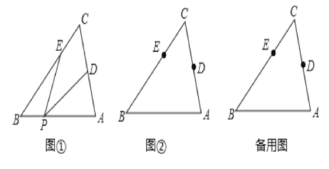
(1)如图①所示,如果点P在线段BA上,且α=30°,那么∠PEB+∠PDA=___;
(2)如图②所示,如果点P在线段BA上运动,
①依据题意补全图形;
②写出∠PEB+∠PDA的大小(用含α的式子表示);并说明理由。
(3)如果点P在线段BA的延长线上运动,直接写出∠PEB与∠PDA之间的数量关系(用含α的式子表示).那么∠PEB与∠PDA之间的数量关系是___.
参考答案:
【答案】(1)90°;(2)①见解析,②60°α;(3)60°+α或60°α或60°;
【解析】
(1)连接PC,由三角形的外角性质即可得出结论;
(2)①根据题意画出图形即可;
②由三角形的外角性质即可得出结论;
(3)分三种情况讨论,由三角形的外角性质即可得出结论.
;(1)∠PEB+∠PDA=90;理由如下;
连接PC,如图1所示
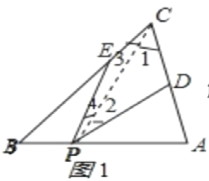
∵∠PEB是△PEC的外角,
∴∠PEB=∠3+∠4,
∵∠PDA是△PDC的外角
∴∠PDA=∠1+∠2,
∴∠PEB+∠PDA=∠1+∠2+∠3+∠4=∠C+∠DPE=60°+30°=90
故答案为:90°;
(2)①如图2所示;
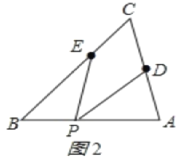
②连接PC,如图3所示:
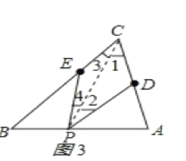
∵∠PEB是△PEC的外角,
∴∠PEB=∠3+∠4,
∵∠PDA是△PDC的外角,
∴∠PDA=∠1+∠2,
∴∠PEB+∠PDA=∠1+∠2+∠3+∠4=∠C+∠DPE=60°+α;
∴∠PEB+∠PDA=60°+α;
(3)分三种情况:
①如图4所示:
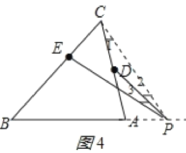
连接PC,
由三角形的外角性质得:
∠PEB=∠ACB+∠1+∠2+∠3,∠PDA=∠1+∠2
∴∠PEB∠PDA=∠ACB+∠3=60°+α;
②如图5所示:连接PC,
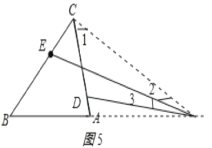
由三角形的外角性质得:
∠PEB=∠ACB+∠1+∠2,∠PDA=∠1+∠2+∠3
∴∠PEB∠PDA=∠ACB∠3=60°α;
③如图6所示:P、D. E在同一条直线上,连接PC,
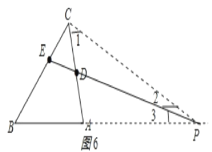
由三角形的外角性质得:
∠PEB=∠ACB+∠1+∠2,∠PDA=∠1+∠2,
∴∠PEB∠PDA=∠ACB=60°;
综上所述:如果点P在线段BA的延长线上运动,
∠PEB与∠PDA之间的数量关系是60°+α或60°α或60°;
故答案为:60°+α或60°α或60°.
-
科目: 来源: 题型:
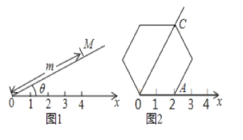
查看答案和解析>>【题目】阅读理如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”。应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校在暑假期间开展“心怀感恩,孝敬父母”的实践活动,倡导学生在假期中帮助父母干家务,开学以后,校学生会随机抽取了部分学生,就暑假“平均每天帮助父母干家务所用时长”进行了调查,以下是根据相关数据绘制的统计图的部分:

根据上述信息,回答下列问题:
 在本次随机抽取的样本中,调查的学生人数是 人;
在本次随机抽取的样本中,调查的学生人数是 人;
 ,
, ;
; 补全频数分布直方图;
补全频数分布直方图; 如果该校共有学生
如果该校共有学生 人,请你估计“平均每天帮助父母干家务的时长不少于
人,请你估计“平均每天帮助父母干家务的时长不少于 分钟”的学生大约有多少人?
分钟”的学生大约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为丰富学生的校园生活,准备从体育用品商店一次性购买若干个篮球和足球(每个篮球的价格相同,每个足球的价格相同).若购买
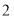 个篮球和
个篮球和 个足球共需
个足球共需 元,购买
元,购买 个篮球和
个篮球和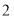 个足球共需
个足球共需 元.
元. 求篮球、足球的单价各是多少元;
求篮球、足球的单价各是多少元; 根据学校实际需要,需一次性购买篮球和足球共
根据学校实际需要,需一次性购买篮球和足球共 个.要求购买篮球和足球的总费用不超过
个.要求购买篮球和足球的总费用不超过 元,则该校最多可以购买多少个篮球?
元,则该校最多可以购买多少个篮球? -
科目: 来源: 题型:
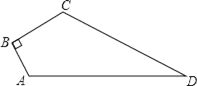
查看答案和解析>>【题目】如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
-
科目: 来源: 题型:
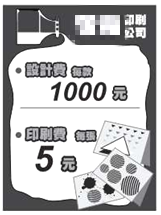
查看答案和解析>>【题目】如图的宣传单为某印刷公司设计与印刷卡片计价方式的说明,小娜打算请此印刷公司设计一款母亲节卡片并印刷,她再将卡片以每张15元的价格贩售.若利润等于收入扣掉成本,且成本只考虑设计费与印刷费,则她至少需印多少张卡片,才可使得卡片全数售出后的利润超过成本的20%?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边型ABCD中,AB∥DC,过对角线AC的中点O作
 ,分别交边AB,CD于点E,F,连接CE,AF.
,分别交边AB,CD于点E,F,连接CE,AF.
(1)求证:四边形AECF是菱形;
(2)若EF=8,AE=5,求四边形AECF的面积.
相关试题

