【题目】在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.
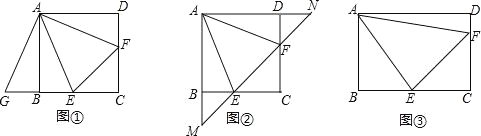
(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;
(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;
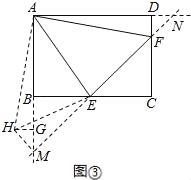
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.
参考答案:
【答案】证明见解析
【解析】
试题分析:(1)根据旋转的性质可知AF=AG,∠EAF=∠GAE=45°,故可证△AEG≌△AEF;
(2)将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.由(1)知△AEG≌△AEF,则EG=EF.再由△BME、△DNF、△CEF均为等腰直角三角形,得出CE=CF,BE=BM,NF=![]() DF,然后证明∠GME=90°,MG=NF,利用勾股定理得出EG2=ME2+MG2,等量代换即可证明EF2=ME2+NF2;
DF,然后证明∠GME=90°,MG=NF,利用勾股定理得出EG2=ME2+MG2,等量代换即可证明EF2=ME2+NF2;
(3)将△ADF绕着点A顺时针旋转90°,得到△ABG,根据旋转的性质可以得到△ADF≌△ABG,则DF=BG,再证明△AEG≌△AEF,得出EG=EF,由EG=BG+BE,等量代换得到EF=BE+DF.
试题解析:(1)∵△ADF绕着点A顺时针旋转90°,得到△ABG,
∴AF=AG,∠FAG=90°,
∵∠EAF=45°,
∴∠GAE=45°,
在△AGE与△AFE中,
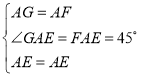 ,
,
∴△AGE≌△AFE(SAS);
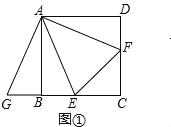
(2)设正方形ABCD的边长为a.
将△ADF绕着点A顺时针旋转90°,得到△ABG,连结GM.
则△ADF≌△ABG,DF=BG.
由(1)知△AEG≌△AEF,
∴EG=EF.
∵∠CEF=45°,
∴△BME、△DNF、△CEF均为等腰直角三角形,
∴CE=CF,BE=BM,NF=![]() DF,
DF,
∴a﹣BE=a﹣DF,
∴BE=DF,
∴BE=BM=DF=BG,
∴∠BMG=45°,
∴∠GME=45°+45°=90°,
∴EG2=ME2+MG2,
∵EG=EF,MG=![]() BM=
BM=![]() DF=NF,
DF=NF,
∴EF2=ME2+NF2;
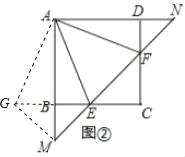
(3)EF2=2BE2+2DF2.
如图所示,延长EF交AB延长线于M点,交AD延长线于N点,
将△ADF绕着点A顺时针旋转90°,得到△AGH,连结HM,HE.
由(1)知△AEH≌△AEF,
则由勾股定理有(GH+BE)2+BG2=EH2,
即(GH+BE)2+(BM﹣GM)2=EH2
又∴EF=HE,DF=GH=GM,BE=BM,所以有(GH+BE)2+(BE﹣GH)2=EF2,
即2(DF2+BE2)=EF2
-
科目: 来源: 题型:
查看答案和解析>>【题目】汽车油箱内存油45L,每行驶100km耗油8L,行驶过程中油箱内剩余油量yL与行驶路程skm的函数关系式是________________________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运用平方差公式计算,错误的是( )
A. (b+a)(a-b)=a2-b2B. (m2+n2)(m2-n2)=m4-n4
C. (2x+1)(2x-1)=2x2-1D. (2-3x)(-3x-2)=9x2-4
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
解答“已知
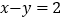 ,且
,且 ,
, ,确定
,确定 的取值范围”有如下解,
的取值范围”有如下解,解:∵
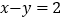 ,
,∴
 .
.又∵
 ,
,∴
 .
.∴
 .
.又∵
 ,
,∴
 ,
, ①
①同理得:
 .
. ②
②由①
 ②得
②得 .
.∴
 的取值范围是
的取值范围是 .
.请按照上述方法,完成下列问题:
(
 )已知
)已知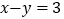 ,且
,且 ,
, ,求
,求 的取值范围.
的取值范围.(
 )已知
)已知 ,
, ,若
,若 ,且
,且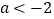 ,求
,求 得取值范围(结果用含
得取值范围(结果用含 的式子表示).
的式子表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】若点(m,n)在函数y=2x-6的图象上,则2m﹣n的值是__________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一座拱桥的轮廓是抛物线型(如图1所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.
(1)将抛物线放在所给的直角坐标系中(如图2所示),其表达式是y=ax2+c的形式.请根据所给的数据求出a,c的值.
(2)求支柱MN的长度.
(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,天星山山脚下西端A处与东端B处相距800(1+
 )米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为
)米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为 米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
相关试题

