【题目】一座拱桥的轮廓是抛物线型(如图1所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.
(1)将抛物线放在所给的直角坐标系中(如图2所示),其表达式是y=ax2+c的形式.请根据所给的数据求出a,c的值.
(2)求支柱MN的长度.
(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由.

参考答案:
【答案】(1)y=-![]() x2+6;(2)5.5米;(3)一条行车道能并排行驶这样的三辆汽车.
x2+6;(2)5.5米;(3)一条行车道能并排行驶这样的三辆汽车.
【解析】试题分析: ![]() 根据题目可知
根据题目可知![]() 的坐标,设出抛物线的解析式代入可求解.
的坐标,设出抛物线的解析式代入可求解.![]() 设
设![]() 点的坐标为
点的坐标为![]() 可求出支柱
可求出支柱![]() 的长度.
的长度.
![]() 设
设![]() 是隔离带的宽,
是隔离带的宽, ![]() 是三辆车的宽度和.作
是三辆车的宽度和.作![]() 垂直
垂直![]() 交抛物线于
交抛物线于![]() ,则可求解.
,则可求解.
试题解析: ![]() 根据题目条件,
根据题目条件, ![]() 的坐标分别是
的坐标分别是![]()
将![]() 的坐标代入
的坐标代入![]() 得
得
![]()
解得![]()
所以抛物线的表达式是![]()
![]() 可设
可设![]() ,于是
,于是![]()
从而支柱![]() 的长度是
的长度是![]() 米.
米.![]() 设
设![]() 是隔离带的宽,
是隔离带的宽, ![]() 是三辆车的宽度和,则
是三辆车的宽度和,则![]() 点坐标是
点坐标是![]()
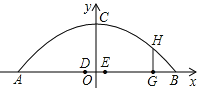
过![]() 点作
点作![]() 垂直
垂直![]() 交抛物线于
交抛物线于![]() ,则
,则![]()
根据抛物线的特点,可知一条行车道能并排行驶这样的三辆汽车.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
解答“已知
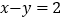 ,且
,且 ,
, ,确定
,确定 的取值范围”有如下解,
的取值范围”有如下解,解:∵
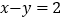 ,
,∴
 .
.又∵
 ,
,∴
 .
.∴
 .
.又∵
 ,
,∴
 ,
, ①
①同理得:
 .
. ②
②由①
 ②得
②得 .
.∴
 的取值范围是
的取值范围是 .
.请按照上述方法,完成下列问题:
(
 )已知
)已知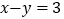 ,且
,且 ,
, ,求
,求 的取值范围.
的取值范围.(
 )已知
)已知 ,
, ,若
,若 ,且
,且 ,求
,求 得取值范围(结果用含
得取值范围(结果用含 的式子表示).
的式子表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.
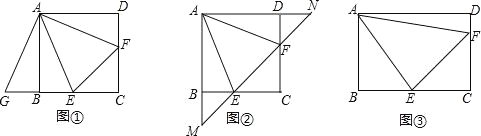
(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;
(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点(m,n)在函数y=2x-6的图象上,则2m﹣n的值是__________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,天星山山脚下西端A处与东端B处相距800(1+
 )米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为
)米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为 米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一个几何体的形状为直三棱柱,右图是它的主视图和左视图.
(1)请补画出它的俯视图,并标出相关数据;
(2)根据图中所标的尺寸(单位:厘米),计算这个几何体的全面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,某超市从一楼到二楼有一自动扶梯,图②是侧面示意图.已知自动扶梯AB的坡度为1∶2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为42°,则二楼的层高BC约为(精确到0.1米,sin42°≈0.67,tan42°≈0.90)( )

A. 10.8米 B. 8.9米 C. 8.0米 D. 5.8米
相关试题

