【题目】已知线段AB⊥直线l于点B,点M在直线l上,分别以AB、AM为边作等边△ABC和等边△AMN,直线CN交直线l于点D.
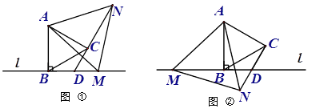
(1)当点M在AB右侧时,如图①,试探索线段CN、CD、DM的数量关系,并说明理由;
(2)当点M在AB左侧时,如图②,(1)中线段CN、CD、DM的数量关系仍然成立吗?若不成立,写出新的数量关系;
(3)若BM=2BD,DN=9,则CD= .
参考答案:
【答案】(1)MD=CN-CD;理由见解析;
(2)(1)中的数量关系不成立,MD=CN+CD;理由见解析;
(3)CD=3或9
【解析】
(1)如图①中,设AM交ND于O.首先证明△ABM≌△ACN(SAS),推出BM=NC,再证明BD=CD即可得到MD=CN-CD;
(2)如图②, 设AM交ND于O.类似(1)的证明方法,先证明△ABM≌△ACN(SAS),得到CN=BM,再证明CD=BD,可得到MD=CN+CD;
(3)分图①,图②两种情形,设BD=CD=x,则BM=2x,列出方程分别求解即可.
(1)MD=CN-CD;理由是:
如图①中,设AM交ND于O.
∵△ABC,△AMN都是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
∴△ABM≌△ACN(SAS),
∴CN=BM,
∴∠ANO=∠DMO,
∵∠AON=∠DOM,
∴∠ODM=∠OAN=60°,
∵AB⊥BC,
∴∠ABM=90°,
∵∠ABC=60°,
∴∠CBD=30°,
∵∠ODM=∠CBD+∠BCD,
∴∠DBC=∠DCB=30°,
∴CD=BD,
∴MD=CN-CD
(2)不成立,MD=CN+CD;
证明:如图②, 设AM交ND于O.

∵△ABC,△AMN都是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
∴△ABM≌△ACN(SAS),
∴CN=BM,
∴∠ANC=∠AMB,
∵∠AOM=∠DON,
∴∠ODN=∠OAM=60°,
∵AB⊥BD,
∴∠ABD=90°,
∵∠ABC=60°,
∴∠CBD=30°,
∵∠ODN=∠CBD+∠BCD,
∴∠DBC=∠DCB=30°,
∴CD=BD,
∴MD=MB+BD=CN+CD;
(3)分两种情况:
①如图①中,

∵BM=2BD,设BD=MD=CD=x,则BM=2x,
∵DN=9,BM=NC,
∴BM+CD=DN
∴2x+x=9,
∴x=3
∴CD=3.
②如图②中,设BD=CD=x,则BM=2x,

∵BM=NC,ND=9,
CD+DN= CN;
∴x+9=2x,
∴x=9,
∴CD=9,
综上所述,CD=3或9.
故答案为3或9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与
与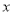 轴交于
轴交于 、
、 两点,
两点, 是以点
是以点 (0,3)为圆心,2为半径的圆上的动点,
(0,3)为圆心,2为半径的圆上的动点,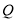 是线段
是线段 的中点,连结
的中点,连结 .则线段
.则线段 的最大值是( )
的最大值是( )
A.
 B.
B.  C.
C. 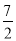 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于( )
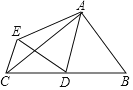
A.2B.
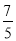 C.
C.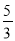 D.
D.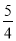
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M.
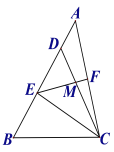
(1)求证:EF=
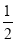 AC.
AC.(2)连接AM,若∠BAC=45°,AM+DM=15,BE=9,求CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l分别与x轴,y轴交于A,B两点,与双曲线(k≠0,x>0)分别交于D,E两点.若点D的坐标为((3.1),点E的坐标为(1,n).
(1)分别求出直线l与双曲线的解析式;
(2)求△EOD的面积;
(3)若将直线l向下平移m(m>O)个单位,当m为何位时,直线l与双曲线有且只有一个交点.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
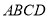 的边长为
的边长为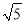 ,
,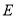 在正方形外,
在正方形外,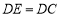 ,过
,过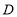 作
作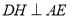 于
于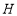 ,直线
,直线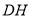 ,
,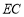 交于点
交于点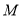 ,直线
,直线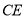 交直线
交直线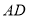 于点
于点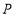 ,则下列结论正确的是( )
,则下列结论正确的是( )
①
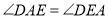 ;②
;②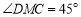 ;③
;③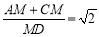 ;
;④若
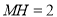 ,则
,则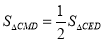
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】曲阜限制“三小车辆”出行后,为方便市民出行,准备为
 、
、 、
、 、
、 四个村建一个公交车站
四个村建一个公交车站 .
.
(1)请问:公交站
 建在何处才能使它到4个村的距离之和
建在何处才能使它到4个村的距离之和 最小,请在图一中找出点
最小,请在图一中找出点 ;
;(2)请问:公交站
 建在何处才能使它到道路
建在何处才能使它到道路 、
、 、
、 的距离相等,请在图二中找出点
的距离相等,请在图二中找出点 并加以说明.
并加以说明.
相关试题

