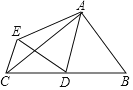
【题目】如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于( )
A.2B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】B
【解析】
如图连接BE交AD于O,作AH⊥BC于H.首先证明AD垂直平分线段BE,△BCE是直角三角形,求出BC、BE,在Rt△BCE中,利用勾股定理即可解决问题.
如图连接BE交AD于O,作AH⊥BC于H.
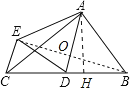
在Rt△ABC中,∵AC=4,AB=3,
∴BC=![]() =5,
=5,
∵CD=DB,
∴AD=DC=DB=![]() ,
,
∵![]() BCAH=
BCAH=![]() ABAC,
ABAC,
∴AH=![]() ,
,
∵AE=AB,DE=DB=DC,
∴AD垂直平分线段BE,△BCE是直角三角形,
∵![]() ADBO=
ADBO=![]() BDAH,
BDAH,
∴OB=![]() ,
,
∴BE=2OB=![]() ,
,
在Rt△BCE中,EC=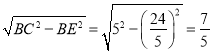
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在数学实践课中测量路灯的高度.如图,已知他的目高
 为1.5米,他先站在
为1.5米,他先站在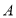 处看路灯顶端
处看路灯顶端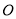 的仰角为
的仰角为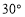 ,向前走3米后站在
,向前走3米后站在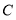 处,此时看灯顶端
处,此时看灯顶端 的仰角为
的仰角为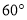 (
(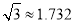 ),则灯顶端
),则灯顶端 到地面的距离约为( )
到地面的距离约为( )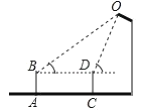
A.3.2米B.4.1米C.4.7米D.5.4米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,反比例函数y=kx-1(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k=_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与
与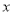 轴交于
轴交于 、
、 两点,
两点, 是以点
是以点 (0,3)为圆心,2为半径的圆上的动点,
(0,3)为圆心,2为半径的圆上的动点,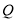 是线段
是线段 的中点,连结
的中点,连结 .则线段
.则线段 的最大值是( )
的最大值是( )
A.
 B.
B.  C.
C. 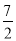 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M.
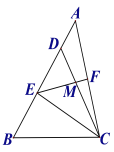
(1)求证:EF=
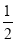 AC.
AC.(2)连接AM,若∠BAC=45°,AM+DM=15,BE=9,求CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB⊥直线l于点B,点M在直线l上,分别以AB、AM为边作等边△ABC和等边△AMN,直线CN交直线l于点D.
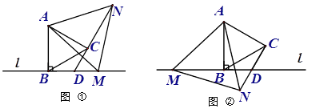
(1)当点M在AB右侧时,如图①,试探索线段CN、CD、DM的数量关系,并说明理由;
(2)当点M在AB左侧时,如图②,(1)中线段CN、CD、DM的数量关系仍然成立吗?若不成立,写出新的数量关系;
(3)若BM=2BD,DN=9,则CD= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l分别与x轴,y轴交于A,B两点,与双曲线(k≠0,x>0)分别交于D,E两点.若点D的坐标为((3.1),点E的坐标为(1,n).
(1)分别求出直线l与双曲线的解析式;
(2)求△EOD的面积;
(3)若将直线l向下平移m(m>O)个单位,当m为何位时,直线l与双曲线有且只有一个交点.

相关试题

