【题目】曲阜限制“三小车辆”出行后,为方便市民出行,准备为![]() 、
、![]() 、
、![]() 、
、![]() 四个村建一个公交车站
四个村建一个公交车站![]() .
.

(1)请问:公交站![]() 建在何处才能使它到4个村的距离之和
建在何处才能使它到4个村的距离之和![]() 最小,请在图一中找出点
最小,请在图一中找出点![]() ;
;
(2)请问:公交站![]() 建在何处才能使它到道路
建在何处才能使它到道路![]() 、
、![]() 、
、![]() 的距离相等,请在图二中找出点
的距离相等,请在图二中找出点![]() 并加以说明.
并加以说明.
参考答案:
【答案】(1)见解析;(2)见解析
【解析】
(1)公交站P是AC与BD的交点,要证这点到四点的距离最小,可以证明除这点以外的点到四点的距离大于这点到四点的距离;
(2)公交站![]() 是∠ABC与∠DCB角平分线的交点,由角平分线性质定理可知,角平分线上的点到这个角两边的距离相等.
是∠ABC与∠DCB角平分线的交点,由角平分线性质定理可知,角平分线上的点到这个角两边的距离相等.
解:(1)应建在AC,BD连线的交点P处,如图一,

理由:如下图,若不建在P处,建在P1处,由三角形两边之和大于第三边可知,
 ,
,
即P1A+P1C+P1B+P1D>AC+BD,
故结论成立应建在P处.
即P1A+P1C+P1B+P1D>AC+BD.
故结论成立应建在P处.
(2)应建在∠ABC与∠DCB角平分线的交点处,如图二,

理由:由角平分线性质定理可知,角平分线上的点到这个角两边的距离相等.
所以点P道路![]() 、
、![]() 、
、![]() 的距离相等.
的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB⊥直线l于点B,点M在直线l上,分别以AB、AM为边作等边△ABC和等边△AMN,直线CN交直线l于点D.
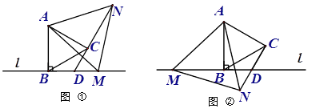
(1)当点M在AB右侧时,如图①,试探索线段CN、CD、DM的数量关系,并说明理由;
(2)当点M在AB左侧时,如图②,(1)中线段CN、CD、DM的数量关系仍然成立吗?若不成立,写出新的数量关系;
(3)若BM=2BD,DN=9,则CD= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l分别与x轴,y轴交于A,B两点,与双曲线(k≠0,x>0)分别交于D,E两点.若点D的坐标为((3.1),点E的坐标为(1,n).
(1)分别求出直线l与双曲线的解析式;
(2)求△EOD的面积;
(3)若将直线l向下平移m(m>O)个单位,当m为何位时,直线l与双曲线有且只有一个交点.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 的边长为
的边长为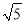 ,
,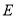 在正方形外,
在正方形外,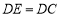 ,过
,过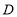 作
作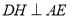 于
于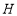 ,直线
,直线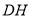 ,
,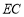 交于点
交于点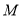 ,直线
,直线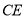 交直线
交直线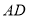 于点
于点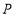 ,则下列结论正确的是( )
,则下列结论正确的是( )
①
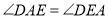 ;②
;②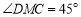 ;③
;③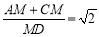 ;
;④若
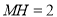 ,则
,则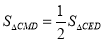
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间
 (时)的关系可近似地用二次函数
(时)的关系可近似地用二次函数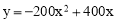 刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数
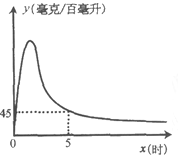
刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数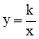 (k>0)刻画(如图所示).
(k>0)刻画(如图所示).(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当
 =5时,y=45.求k的值.
=5时,y=45.求k的值.(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
-
科目: 来源: 题型:
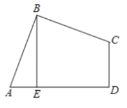
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为144,则BE________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P在正方形ABCD边AD上,连接PB,过点B作一条射线与边DC的延长线交于点 Q,使得∠QBE=∠PBC,其中E是边AB延长线上的点,连接PQ,若PQ=PB+PD+3,则△PAB的面积为____.

相关试题

