【题目】如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M.
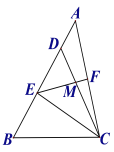
(1)求证:EF=![]() AC.
AC.
(2)连接AM,若∠BAC=45°,AM+DM=15,BE=9,求CE的长.
参考答案:
【答案】(1)见解析;(2)CE=12.
【解析】
(1)根据等腰三角形三线合一的性质可得CE⊥BD,再根据直角三角形斜边上的中线等于斜边的一半可得EF= ![]() AC;
AC;
(2)连接AM,证得△AEC是等腰直角三角形,EF垂直平分AC,AM=CM,则BC=AM+DM=15,在Rt△BEC中,利用勾股定理可得出CE的长。
(1)证明:
∵CD=CB,点E为BD的中点,
∴CE⊥BD,
∴∠AEC=90°,
∵在Rt△AEC中,点F为AC的中点,
∴EF=![]() AC;
AC;
(2)如图,连接AM,
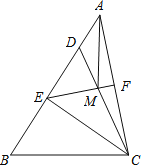
∵∠BAC=45°,CE⊥BD,
∴△AEC是等腰直角三角形,
∵点F为AC的中点,
∴EF垂直平分AC,
∴AM=CM,
∵CD=CM+DM=AM+DM,CD=CB,
∴BC=AM+DM=15,
∵BE=9,
在Rt△BEC中,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,反比例函数y=kx-1(x>0)的图象交矩形OABC的边AB于点D,交边BC于点E,且BE=2EC.若四边形ODBE的面积为6,则k=_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与
与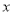 轴交于
轴交于 、
、 两点,
两点, 是以点
是以点 (0,3)为圆心,2为半径的圆上的动点,
(0,3)为圆心,2为半径的圆上的动点,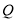 是线段
是线段 的中点,连结
的中点,连结 .则线段
.则线段 的最大值是( )
的最大值是( )
A.
 B.
B.  C.
C. 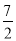 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=90°,AB=3,AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连CE,则线段CE的长等于( )
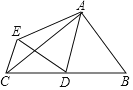
A.2B.
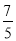 C.
C.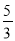 D.
D.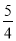
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段AB⊥直线l于点B,点M在直线l上,分别以AB、AM为边作等边△ABC和等边△AMN,直线CN交直线l于点D.
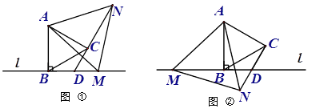
(1)当点M在AB右侧时,如图①,试探索线段CN、CD、DM的数量关系,并说明理由;
(2)当点M在AB左侧时,如图②,(1)中线段CN、CD、DM的数量关系仍然成立吗?若不成立,写出新的数量关系;
(3)若BM=2BD,DN=9,则CD= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l分别与x轴,y轴交于A,B两点,与双曲线(k≠0,x>0)分别交于D,E两点.若点D的坐标为((3.1),点E的坐标为(1,n).
(1)分别求出直线l与双曲线的解析式;
(2)求△EOD的面积;
(3)若将直线l向下平移m(m>O)个单位,当m为何位时,直线l与双曲线有且只有一个交点.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 的边长为
的边长为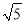 ,
,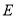 在正方形外,
在正方形外,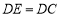 ,过
,过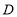 作
作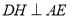 于
于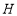 ,直线
,直线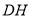 ,
,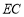 交于点
交于点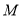 ,直线
,直线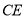 交直线
交直线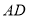 于点
于点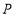 ,则下列结论正确的是( )
,则下列结论正确的是( )
①
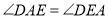 ;②
;②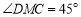 ;③
;③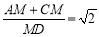 ;
;④若
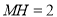 ,则
,则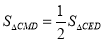
A.1个B.2个C.3个D.4个
相关试题

