搜索
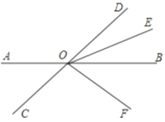
【题目】如图，直线AB、CD相交于点O，OE平分∠BOD，OF平分∠COE．∠BOF=30°，求∠BOE的度数．
参考答案：
【答案】40°
【解析】
设∠BOE=x，由角平分线的定义可得：∠DOE=∠BOE =x，由已知可得：∠EOF=x＋30°，再根据角平分线的定义可得：∠COE=2∠EOF= 2x＋60°，最后根据∠DOE＋∠COE=180°列方程并解方程即可.
解：设∠BOE=x
∵OE平分∠BOD，
∴∠DOE=∠BOE =x
∵∠BOF=30°
∴∠EOF=∠BOE＋∠BOF=x＋30°
∵OF平分∠COE
∴∠COE=2∠EOF= 2x＋60°
∵∠DOE＋∠COE=180°
∴x＋（2x＋60°）=180°
解得：x=40°
即∠BOE=40°
-
科目： 来源： 题型：
查看答案和解析>>【题目】某学校为了解本校八年级学生生物考试测试情况，随机抽取了本校八年级部分学生的生物测试成绩为样本，按A（优秀）、B（良好）、C（合格）、D（不合格）四个等级进行统计，并将统计结果绘制成如下统计图表．请你结合图表中所给信息解答下列问题：
等级
人数
A（优秀）
40
B（良好）
80
C（合格）
70
D（不合格）
（1）请将上面表格中缺少的数据补充完整；
（2）扇形统计图中“A”部分所对应的圆心角的度数是 ；
（3）该校八年级共有1200名学生参加了身体素质测试，试估计测试成绩合格以上（含合格）的人数．
-
科目： 来源： 题型：
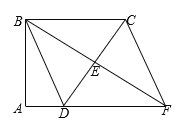
查看答案和解析>>【题目】如图，四边形ABCD中，∠A=∠ABC=90°，E是边CD的中点，连接BE并延长与AD的延长线相交于点F，连接CF．四边形BDFC是平行四边形吗？证明你的结论．
-
科目： 来源： 题型：
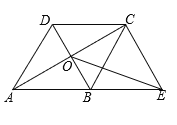
查看答案和解析>>【题目】在四边形ABCD中，AB∥DC，AB=AD，对角线AC，BD交于点O，AC平分∠BAD，过点C作CE∥DB交AB的延长线于点E，连接OE．
（1）求证：四边形ABCD是菱形；
（2）若∠DAB=60°，且AB=4，求OE的长．
-
科目： 来源： 题型：
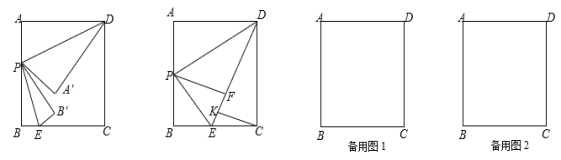
查看答案和解析>>【题目】如图，在矩形ABCD中，AB＝8，BC＝6，点P、点E分别是边AB、BC上的动点，连结DP、PE．将△ADP与△BPE分别沿DP与PE折叠，点A与点B分别落在点A′，B′处．
(1) 当点P运动到边AB的中点处时，点A′与点B′重合于点F处，过点C作CK⊥EF于K，求CK的长；
(2) 当点P运动到某一时刻，若P，A'，B'三点恰好在同一直线上，且A'B'＝4 ，试求此时AP的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，己知线段AB=20cm，CD=2cm，线段
在线段
上运动，
分别是AC，BC的中点.(1)若
=4cm，则
=______cm.(2)当线段
在线段上运动时，试判断的长度是否发生变化?如果不变请求出的长度，如果变化，请说明理由. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，线段AB和射线BM交于点B．
（1）利用尺规完成以下作图，并保留作图痕迹（不写作法）
①在射线BM上作一点C，使AC=AB；
②作∠ABM 的角平分线交AC于D点；
③在射线CM上作一点E，使CE=CD，连接DE.
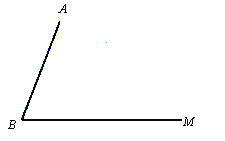
（2）在（1）所作的图形中，猜想线段BD与DE的数量关系，并证明之．
相关试题
