【题目】如图,己知线段AB=20cm,CD=2cm,线段![]() 在线段
在线段![]() 上运动,
上运动,![]() 分别是AC,BC的中点.
分别是AC,BC的中点.
(1)若![]() =4cm,则
=4cm,则![]() =______cm.
=______cm.
(2)当线段![]() 在线段
在线段![]() 上运动时,试判断
上运动时,试判断![]() 的长度是否发生变化?如果不变请求出
的长度是否发生变化?如果不变请求出![]() 的长度,如果变化,请说明理由.
的长度,如果变化,请说明理由.
![]()
参考答案:
【答案】(1)10;(2)不变,EF=10,理由见解析.
【解析】
(1)由已知条件先求出BC的长,再根据中点的定义分别求出EC、CF,即可求出EF的长;
(2)不变,由已知条件先用AC表示出BC,再根据中点的定义求出EC、CF,从而求出EF的长.
解:(1)∵AB=20cm,![]() =4cm,
=4cm,
∴BC= AB-AC =16cm
∵![]() 分别是AC,BC的中点
分别是AC,BC的中点
∴EC=![]() AC=2cm,CF=
AC=2cm,CF=![]() BC=8cm
BC=8cm
∴![]()
(2)不变,理由如下
∵AB=20cm,
∴BC= AB-AC=20-AC
∵![]() 分别是AC,BC的中点
分别是AC,BC的中点
∴EC=![]() AC,CF=
AC,CF=![]() BC=
BC=![]() (20-AC)=10-
(20-AC)=10-![]() AC
AC
∴![]()
即当线段![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 的长度不变.
的长度不变.
-
科目: 来源: 题型:
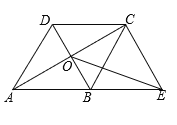
查看答案和解析>>【题目】在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE∥DB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若∠DAB=60°,且AB=4,求OE的长.
-
科目: 来源: 题型:
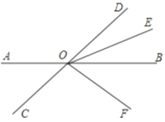
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.∠BOF=30°,求∠BOE的度数.
-
科目: 来源: 题型:
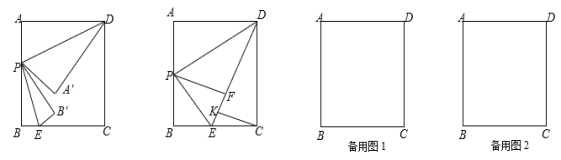
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,BC=6,点P、点E分别是边AB、BC上的动点,连结DP、PE.将△ADP与△BPE分别沿DP与PE折叠,点A与点B分别落在点A′,B′处.
(1) 当点P运动到边AB的中点处时,点A′与点B′重合于点F处,过点C作CK⊥EF于K,求CK的长;
(2) 当点P运动到某一时刻,若P,A',B'三点恰好在同一直线上,且A'B'=4 ,试求此时AP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,线段AB和射线BM交于点B.
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法)
①在射线BM上作一点C,使AC=AB;
②作∠ABM 的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.
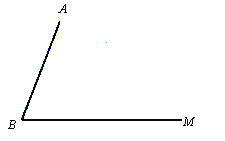
(2)在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明之.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解“阳光体育”活动的开展情况,从全校2000名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.
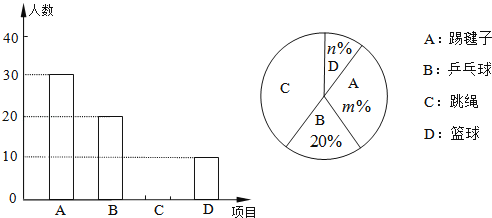
根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,m= ,n= ,表示区域C的圆心角为 度;
(3)全校学生中喜欢篮球的人数大约有多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装公司招工广告承诺:熟练工人每月工资至少4000元.每天工作8小时,一个月工作25天.月工资底薪1000元,另加计件工资.加工1件A型服装计酬20元,加工1件B型服装计酬15元.在工作中发现一名熟练工加工2件A型服装和3件B型服装需7小时,加工1件A型服装和2件B型服装需4小时.(工人月工资=底薪+计件工资)
(1)一名熟练工加工1件A型服装和1件B型服装各需要多少小时?
(2)一段时间后,公司规定:“每名工人每月必须加工A,B两种型号的服装,且加工A型服装数量不少于B型服装的一半”.设一名熟练工人每月加工A型服装a件,工资总额为W元.请你运用所学知识判断该公司在执行规定后是否违背了广告承诺?
相关试题

