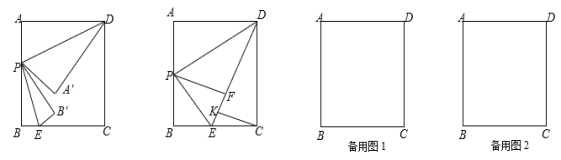
【题目】如图,在矩形ABCD中,AB=8,BC=6,点P、点E分别是边AB、BC上的动点,连结DP、PE.将△ADP与△BPE分别沿DP与PE折叠,点A与点B分别落在点A′,B′处.
(1) 当点P运动到边AB的中点处时,点A′与点B′重合于点F处,过点C作CK⊥EF于K,求CK的长;
(2) 当点P运动到某一时刻,若P,A',B'三点恰好在同一直线上,且A'B'=4 ,试求此时AP的长.
参考答案:
【答案】(1)![]() ;(2),PA的长为2或6.
;(2),PA的长为2或6.
【解析】
(1)由折叠的性质可得E ,F,D三点在同一直线上,在Rt△DEC中,根据勾股定理可求出BE,CE,DE的长,再根据面积法即可求出CK的值;
(2)分两种情况进行讨论:根据A′B′=4列出方程求解即可.
⑴如图,

∵四边形ABCD为矩形,将△ADP与△BPE分别沿DP与PE折叠,
∴∠PFD=∠PFE=90°,
∴∠PFD+∠PFE=180°,即:E ,F,D三点在同一直线上.
设BE=EF=x,则EC=6-x,
∵DC=AB=8, DF=AD=6,
在Rt△DEC中,∵DE=DF+FE=6+x, EC=6-x, DC=8,
∴(6+x)2=(6-x)2+82,
计算得出x=![]() ,即BE=EF=
,即BE=EF=![]() ,
,
∴DE=![]() , EC=
, EC=![]() ,
,
∵S△DCE=![]() DCCE=
DCCE=![]() DECK,
DECK,
∴CK=![]() ;
;
⑵①如图2中,设AP=x,则PB=8-x,
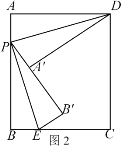
由折叠可知:PA′=PA=x , PB′=PB=8-x,
∵A′B′=4,
∴8-x-x=4,
∴x=2, 即AP=2.
②如图3中,
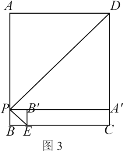
∵A′B′=4,
∴x-(8-x)=4, ∴x=6, 即AP=6.
综上所述,PA的长为2或6.
-
科目: 来源: 题型:
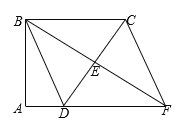
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠ABC=90°,E是边CD的中点,连接BE并延长与AD的延长线相交于点F,连接CF.四边形BDFC是平行四边形吗?证明你的结论.
-
科目: 来源: 题型:
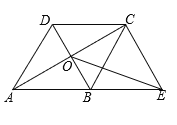
查看答案和解析>>【题目】在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE∥DB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若∠DAB=60°,且AB=4,求OE的长.
-
科目: 来源: 题型:
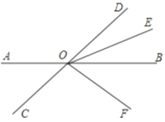
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE平分∠BOD,OF平分∠COE.∠BOF=30°,求∠BOE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,己知线段AB=20cm,CD=2cm,线段
 在线段
在线段 上运动,
上运动, 分别是AC,BC的中点.
分别是AC,BC的中点.(1)若
 =4cm,则
=4cm,则 =______cm.
=______cm.(2)当线段
 在线段
在线段 上运动时,试判断
上运动时,试判断 的长度是否发生变化?如果不变请求出
的长度是否发生变化?如果不变请求出 的长度,如果变化,请说明理由.
的长度,如果变化,请说明理由. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,线段AB和射线BM交于点B.
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法)
①在射线BM上作一点C,使AC=AB;
②作∠ABM 的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.
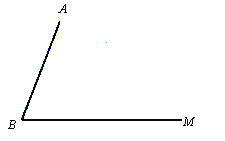
(2)在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明之.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了解“阳光体育”活动的开展情况,从全校2000名学生中,随机抽取部分学生进行问卷调查(每名学生只能填写一项自己喜欢的活动项目),并将调查结果绘制成如下两幅不完整的统计图.
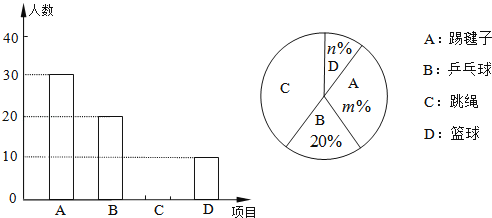
根据以上信息,解答下列问题:
(1)被调查的学生共有 人,并补全条形统计图;
(2)在扇形统计图中,m= ,n= ,表示区域C的圆心角为 度;
(3)全校学生中喜欢篮球的人数大约有多少?
相关试题

