【题目】如图,点![]() 、
、![]() 分别在射线
分别在射线![]() 、
、![]() 上运动(不与点
上运动(不与点![]() 重合).
重合).
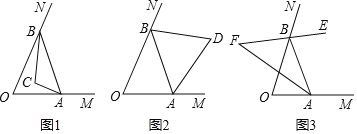
(1)如图1,若![]() ,
,![]() 、
、![]() 的平分线交于点
的平分线交于点![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,若![]() ,
,![]() 的外角
的外角![]() 、
、![]() 的平分线交于点
的平分线交于点![]() ,则
,则![]() 等于______度(用含字母
等于______度(用含字母![]() 的代数式表示);
的代数式表示);
(3)如图3,若![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() 的反向延长线与
的反向延长线与![]() 的平分线交于点
的平分线交于点![]() .试问:随着点
.试问:随着点![]() 、
、![]() 的运动,
的运动,![]() 的大小会变吗?如果不会,求
的大小会变吗?如果不会,求![]() 的度数;如果会,请说明理由.
的度数;如果会,请说明理由.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 的度数不变,
的度数不变,![]() ;理由见解析.
;理由见解析.
【解析】
(1)根据三角形内角和定理得到∠OBA+∠OAB=110°,根据角平分线的定义计算即可;
(2)根据三角形内角和定理得到∠NBA+∠MAB=180°+n°,根据角平分线的定义计算即可;
(3)根据三角形的外角性质得到∠NBA﹣∠BAO=∠MON=70°,根据角平分线的定义、三角形的外角性质计算即可.
(1)∵∠MON=70°,∴∠OBA+∠OAB=180°﹣70°=110°.
∵BC、AC分别为∠OBA、∠OAB的平分线,∴∠ABC![]() ∠OBA,∠BAC
∠OBA,∠BAC![]() ∠OAB,∴∠ABC+∠BAC
∠OAB,∴∠ABC+∠BAC![]() (∠OBA+∠OAB)=55°,∴∠ACB=180°﹣55°=125°;
(∠OBA+∠OAB)=55°,∴∠ACB=180°﹣55°=125°;
(2)∵∠MON=n°,∴∠OBA+∠OAB=180°﹣n°,∴∠NBA+∠MAB=360°-(180°-n°)=180°+n°.
∵BD、AD分别为∠NBA、∠MAB的平分线,∴∠DBA![]() ∠NBA,∠DAB
∠NBA,∠DAB![]() ∠MAB,∴∠DBA+∠DAB
∠MAB,∴∠DBA+∠DAB![]() (∠NBA+∠MAB)=90°
(∠NBA+∠MAB)=90°![]() n°,∴∠ADB=180°﹣(90°
n°,∴∠ADB=180°﹣(90°![]() n°)=90°
n°)=90°![]() n°.
n°.
故答案为:90![]() n;
n;
(3)∠F的大小不变,理由如下:
∵BE是∠ABN的平分线,AF是∠OAB的平分线,∴∠EBA![]() ∠NBA,∠BAF
∠NBA,∠BAF![]() ∠BAO.
∠BAO.
∵∠NBA﹣∠BAO=∠MON=70°,∴∠F=∠EBA﹣∠BAF![]() (∠NBA﹣∠BAO)=35°.
(∠NBA﹣∠BAO)=35°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在前面学习中,一些乘法公式可以通过几何图形来进行验证,请结合下列两组图形回答问题:

图①说明:左侧图形中阴影部分由右侧阴影部分分割后拼接而成.
图②说明:边长为
 的正方形的面积分割成如图所示的四部分.
的正方形的面积分割成如图所示的四部分.(1)请结合图①和图②分别写出学过的两个乘法公式:
图①:____________,图②:____________;
(2)请利用上面的乘法公式计算:
①
 ;
; ②
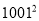
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面直角坐标系中有一点
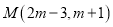 .
.(1)若点
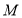 到
到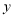 轴的距离为2时,求点
轴的距离为2时,求点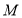 的坐标;
的坐标;(2)若点
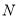 的坐标是
的坐标是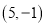 ,当
,当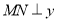 轴时,求点
轴时,求点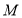 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=2,AC=
 ,∠BAC=105°,△ABD,△ACE,△BCF都是等边三角形,则四边形AEFD的面积为__________.
,∠BAC=105°,△ABD,△ACE,△BCF都是等边三角形,则四边形AEFD的面积为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】20筐白菜,以每筐18千克为标准,超过或不足的千克数分别用正、负数来表示.记录如下:
与标准质量的差值(单位:千克)
 3
3 2
2 1.5
1.50
1
2.5
筐数
2
3
2
1
4
8
(1)20筐白菜中,最重的一筐比最轻的一筐重 千克.
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价1.3元,则出售这20筐白菜可卖多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.

(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两地相距360千米,一辆贩毒车从甲地往乙地接头取货,警方截取情报后,立即组织干警从甲地出发,前往乙地缉拿这伙犯罪分子,结果警车与贩毒车同时到达,将犯罪分子一网打尽.已知贩毒车比警车早出发1小时15分,警车与贩毒车的速度比为4∶3,求贩毒车和警车的速度.
相关试题

