【题目】如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.

(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值.
参考答案:
【答案】(1) t=1或![]() ;(2)
;(2) ![]()
【解析】试题分析:
(1)由∠B是△BPQ与△ABC的公共角,可知,若两三角形相似,存在两种情况:①△BPQ∽△BAC;②△BPQ∽△BCA;分这两种情况结合相似三角形的性质和题意即可解得对应的t的值;
(2)如图1,过P作PM⊥BC于点M,AQ,CP交于点N,由题意可知:当AQ⊥CP时,△ACQ∽△CMP,由相似三角形的性质列出比例式即可解得对应的t的值.
试题解析:
(1)∵Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,
∴由勾股定理可得:BA=![]() ;
;
由题意现分两种情况讨论:
①当△BPQ∽△BAC时, ![]() ,
,
∵BP=5t,QC=4t,AB=10,BC=8,
∴![]() ,解得:
,解得: ![]() ;
;
②当△BPQ∽△BCA时, ![]() ,
,
∴![]() ,解得,
,解得, ![]() ;
;
综上所述,当![]() 或
或![]() 时,△BPQ与△ABC相似.
时,△BPQ与△ABC相似.
(2)过P作PM⊥BC于点M,AQ,CP交于点N,如图1所示:

∴∠PMB=∠ACB=90°,
∴PM∥AC,
∴△BPM∽△BAC,
∴![]() ,即
,即![]() ,
,
∴PM=![]() ,BM=
,BM=![]() ,
,
∴CM=![]() .
.
∵AQ⊥CP,∠ACB=90°,
∵∠NAC+∠NCA=90°,∠PCM+∠NCA=90°,
∴∠NAC=∠PCM,
∵∠ACQ=∠PMC,
∴△ACQ∽△CMP,
∴![]() ,即
,即![]() ,解得
,解得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=2,AC=
 ,∠BAC=105°,△ABD,△ACE,△BCF都是等边三角形,则四边形AEFD的面积为__________.
,∠BAC=105°,△ABD,△ACE,△BCF都是等边三角形,则四边形AEFD的面积为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
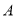 、
、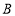 分别在射线
分别在射线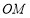 、
、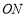 上运动(不与点
上运动(不与点 重合).
重合).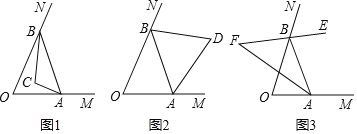
(1)如图1,若
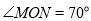 ,
, 、
、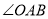 的平分线交于点
的平分线交于点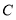 ,求
,求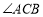 的度数;
的度数;(2)如图2,若
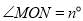 ,
,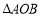 的外角
的外角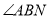 、
、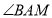 的平分线交于点
的平分线交于点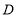 ,则
,则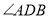 等于______度(用含字母
等于______度(用含字母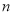 的代数式表示);
的代数式表示);(3)如图3,若
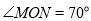 ,
,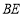 是
是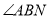 的平分线,
的平分线,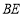 的反向延长线与
的反向延长线与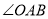 的平分线交于点
的平分线交于点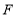 .试问:随着点
.试问:随着点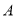 、
、 的运动,
的运动, 的大小会变吗?如果不会,求
的大小会变吗?如果不会,求 的度数;如果会,请说明理由.
的度数;如果会,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】20筐白菜,以每筐18千克为标准,超过或不足的千克数分别用正、负数来表示.记录如下:
与标准质量的差值(单位:千克)
 3
3 2
2 1.5
1.50
1
2.5
筐数
2
3
2
1
4
8
(1)20筐白菜中,最重的一筐比最轻的一筐重 千克.
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价1.3元,则出售这20筐白菜可卖多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两地相距360千米,一辆贩毒车从甲地往乙地接头取货,警方截取情报后,立即组织干警从甲地出发,前往乙地缉拿这伙犯罪分子,结果警车与贩毒车同时到达,将犯罪分子一网打尽.已知贩毒车比警车早出发1小时15分,警车与贩毒车的速度比为4∶3,求贩毒车和警车的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】九年级某班从A、B、C、D四位同学中选出两名同学去参加学校的羽毛球双打比赛.
(1)请用树状图法,求恰好选中A、C两位同学的概率;
(2)若已确定B被选中,再从其余三位同学中随机选取一位,求恰好选中C同学的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G,连接DG.

(1)求证:四边形DEFG为菱形;
(2)若CD=8,CF=4,求
 的值.
的值.
相关试题

