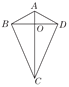
【题目】两组邻边分别相等的四边形我们称它为筝形.如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O,下列判断正确的有_____(填序号).
①AC⊥BD;②AC,BD互相平分;③AC平分∠BCD;④∠ABC=∠ADC=90°;⑤筝形ABCD的面积为![]() AC·BD.
AC·BD.
参考答案:
【答案】①③⑤
【解析】
根据题意AB=AD,BC=DC,AC与BD相交于点O可以证明△ABC≌△ADC、△ABO≌△ADO,可得AC、BD互相垂直,AC平分∠BAD、∠BCD.
∵在△ABC与△ADC中, ,∴△ABC≌△ADC(SSS),∴∠BAO=∠DAO,∠BCO=∠DCO,即AC平分∠BCD.故③正确;
,∴△ABC≌△ADC(SSS),∴∠BAO=∠DAO,∠BCO=∠DCO,即AC平分∠BCD.故③正确;
∵AC平分∠BAD、∠BCD,△ABD与△BCD均为等腰三角形,∴AC、BD互相垂直,但不平分.故①正确,②错误;
由题中条件无法证明∠ABC=∠ADC=90°,故④错误;
∵AC、BD互相垂直,∴筝形ABCD的面积为:![]() ACBO
ACBO![]() ACOD
ACOD![]() ACBD.
ACBD.
故⑤正确;
综上所述:正确的说法是①③⑤.
故答案为:①③⑤.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AC=BC,∠ACB=90°,点 D,E分别在AB,BC上,且AD=BE,BD=AC,过E作EF⊥AB于F.
(1)求证:∠FED=∠CED;
(2)若 BF=
 ,直接写出 CE的长为_______.
,直接写出 CE的长为_______.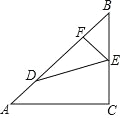
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=
 x与双曲线y=
x与双曲线y= 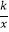 的交点A的横坐标为2
的交点A的横坐标为2
(1)求k的值
(2)如图,过点P(m,3)(m>0)作x轴的垂线交双曲线y=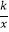 (x>0)于点M,交直线OA于点N
(x>0)于点M,交直线OA于点N 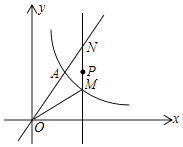
①连接OM,当OA=OM时,直接写出PN﹣PM的值
②试比较PM与PN的大小,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,∠BAD=α,∠BCD=180°﹣α,BD平分∠ABC.
(1)如图,若α=90°,根据教材中一个重要性质直接可得 DA=CD,这个性质是__________.
(2)问题解决:如图,求证AD=CD;
(3)问题拓展:如图,在等腰△ABC中,∠BAC=100°,BD平分∠ABC,求证:BD+AD=BC.
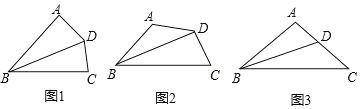
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若∠A=15°,AB=BC=CD=DE=EF,则∠DEF等于__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,然后解决问题:和、差、倍、分等问题中有着广泛的应用,截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段,或将某条线段延长,使之与某特定线段相等,再利用全等三角形的性质等有关知识来解决数学问题.
(1)如图1,在△ABC中,若 AB=12,AC=8,求 BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使 DE=AD,再连接 BE,把AB、AC、2AD集中在△ABE中.利用三角形三边的关系即可判断中线 AD的取值范围是_______.
问题解决:
(2)如图2,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E、F分别是边BC,CD上的两点,且∠EAF=
 ∠BAD,求证:BE+DF=EF.
∠BAD,求证:BE+DF=EF.问题拓展:
(3)如图3,在△ABC中,∠ACB=90°,∠CAB=60°,点D是△ABC 外角平分线上一点,DE⊥AC交 CA延长线于点E,F是 AC上一点,且DF=DB.
求证:AC﹣AE=
 AF.
AF.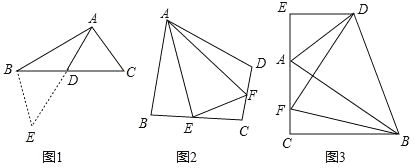
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正六边形ABCDEF中,N、M为边上的点,BM、AN相交于点P

(1)如图1,若点N在边BC上,点M在边DC上,BN=CM,求证:BPBM=BNBC;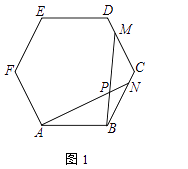
(2)如图2,若N为边DC的中点,M在边ED上,AM∥BN,求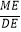 的值;
的值;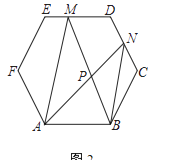
(3)如图3,若N、M分别为边BC、EF的中点,正六边形ABCDEF的边长为2,请直接写出AP的长.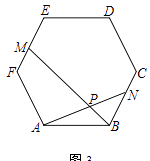
相关试题

