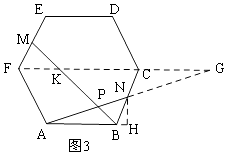
【题目】在正六边形ABCDEF中,N、M为边上的点,BM、AN相交于点P
(1)如图1,若点N在边BC上,点M在边DC上,BN=CM,求证:BPBM=BNBC;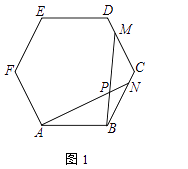
(2)如图2,若N为边DC的中点,M在边ED上,AM∥BN,求 ![]() 的值;
的值;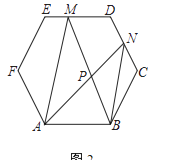
(3)如图3,若N、M分别为边BC、EF的中点,正六边形ABCDEF的边长为2,请直接写出AP的长.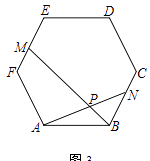
参考答案:
【答案】
(1)
证明:在正六边形ABCDEF中,AB=BC,∠ABC=∠BCD=120°,
∵BN=CM,
∴△ABN≌△BCM,
∴∠ANB=∠BMC,
∵∠PBN=∠CBM,
∴△BPN∽△BCM,
∴ ![]() =
= ![]() ,
,
∴BPBM=BNBC;
(2)
解:延长BC,ED交于点H,延长BN交DH于点G,取BG的中点K,连接KC,
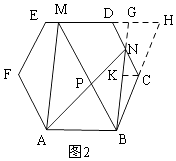
在正六边形ABCDEF中,∠BCD=∠CDE=120°,
∴∠HCD=∠CDH=60°,
∴∠H=60°,
∴DC=DH=CH,
∵DC=BC,
∴CH=BC,
∵BK=GK,
∴2KC=GH,KC∥DH,
∴∠GDN=∠KCN,
∵CN=DN,∠DNG=∠CNK,
∴△DNG≌△CNK,
∴KC=DG,
∴DG= ![]() DH=
DH= ![]() DE,
DE,
∵MG∥AB,AM∥BG,
∴四边形MABG是平行四边形,
∴MG=AB=ED,
∴ME=DG= ![]() DE,即
DE,即 ![]() =
= ![]() ,
,
(3)
解:如图3,过N作NH⊥AB,交AB的延长线于H,
∵∠ABC=120°,
∴∠NBH=60°,
Rt△NBH中,∠BNH=30°,BN=1,
∴BH= ![]() BN=
BN= ![]() ,
,
∴NH= ![]() =
= ![]() ,
,
Rt△ANH中,AN= ![]() =
= ![]() =
= ![]() ,
,
连接FC,延长FC与AN交于G,设FC与BM交于K,
易证△ANB≌△GNC,
∴CG=AB=2,AN=NG= ![]() ,FC=2AB=4,
,FC=2AB=4,
∴FG=FC+CG=6,
∵EF∥BC,
∴ ![]() ,
,
∴ ![]() ,
,
∵FK+KC=6,
∴FK= ![]() ,KC=
,KC= ![]() ,KG=
,KG= ![]() +2=
+2= ![]() ,
,
∵KG∥AB,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
设PG=7x,AP=3x,
由PG+AP=AG=2 ![]() 得:7x+3x=2
得:7x+3x=2 ![]() ,
,
x= ![]() ,
,
∴AP=3x= ![]() .
.
【解析】(1)先证明△ABN≌△BCM,得∠ANB=∠BMC,再证明△BPN∽△BCM,列比例式可得结论;(2)作辅助线,构建等边三角形的三角形的中位线CK,先证明△CDH是等边三角形得:∠HCD=∠CDH=∠H=60°,DC=DH=CH,由△DNG≌△CNK,得KC=DG,DG= ![]() DH=
DH= ![]() DE,利用四边形MABG是平行四边形,
DE,利用四边形MABG是平行四边形,
得MG=AB=ED,所以ME=DG= ![]() DE,即
DE,即 ![]() =
= ![]() ;(3)如图3,作辅助线,构建直角三角形和全等三角形,根据直角三角形30°的性质得:BH=
;(3)如图3,作辅助线,构建直角三角形和全等三角形,根据直角三角形30°的性质得:BH= ![]() ,NH=
,NH= ![]() ,利用勾股定理求AN=
,利用勾股定理求AN= ![]() ,证明△ANB≌△GNC,利用EF∥BC和KG∥AB,列比例式可得:
,证明△ANB≌△GNC,利用EF∥BC和KG∥AB,列比例式可得: ![]() =
= ![]() ,设PG=7x,AP=3x,根据PG+AP=AG=2
,设PG=7x,AP=3x,根据PG+AP=AG=2 ![]() 得:7x+3x=2
得:7x+3x=2 ![]() ,可得结论.
,可得结论.
【考点精析】利用相似三角形的应用对题目进行判断即可得到答案,需要熟知测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两组邻边分别相等的四边形我们称它为筝形.如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O,下列判断正确的有_____(填序号).
①AC⊥BD;②AC,BD互相平分;③AC平分∠BCD;④∠ABC=∠ADC=90°;⑤筝形ABCD的面积为
 AC·BD.
AC·BD.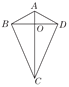
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若∠A=15°,AB=BC=CD=DE=EF,则∠DEF等于__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,然后解决问题:和、差、倍、分等问题中有着广泛的应用,截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段,或将某条线段延长,使之与某特定线段相等,再利用全等三角形的性质等有关知识来解决数学问题.
(1)如图1,在△ABC中,若 AB=12,AC=8,求 BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使 DE=AD,再连接 BE,把AB、AC、2AD集中在△ABE中.利用三角形三边的关系即可判断中线 AD的取值范围是_______.
问题解决:
(2)如图2,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E、F分别是边BC,CD上的两点,且∠EAF=
 ∠BAD,求证:BE+DF=EF.
∠BAD,求证:BE+DF=EF.问题拓展:
(3)如图3,在△ABC中,∠ACB=90°,∠CAB=60°,点D是△ABC 外角平分线上一点,DE⊥AC交 CA延长线于点E,F是 AC上一点,且DF=DB.
求证:AC﹣AE=
 AF.
AF.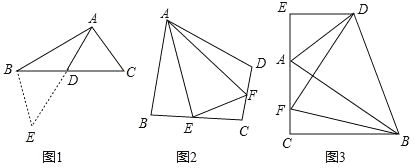
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线y=
 x2经过点A(x1 , y1)、C(x2 , y2),其中x1、x2是方程x2﹣2x﹣8的两根,且x1<x2 , 过点A的直线l与抛物线只有一个公共点
x2经过点A(x1 , y1)、C(x2 , y2),其中x1、x2是方程x2﹣2x﹣8的两根,且x1<x2 , 过点A的直线l与抛物线只有一个公共点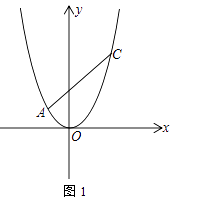
(1)求A、C两点的坐标;
(2)求直线l的解析式;
(3)如图2,点B是线段AC上的动点,若过点B作y轴的平行线BE与直线l相交于点E,与抛物线相交于点D,过点E作DC的平行线EF与直线AC相交于点F,求BF的长.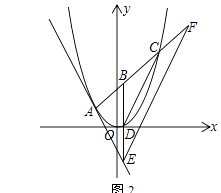
-
科目: 来源: 题型:
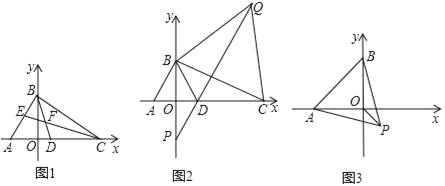
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣3,0),点 B是 y轴正半轴上一动点,点C、D在 x正半轴上.
(1)如图,若∠BAO=60°,∠BCO=40°,BD、CE 是△ABC的两条角平分线,且BD、CE交于点F,直接写出CF的长_____.
(2)如图,△ABD是等边三角形,以线段BC为边在第一象限内作等边△BCQ,连接 QD并延长,交 y轴于点 P,当点 C运动到什么位置时,满足 PD=
 DC?请求出点C的坐标;
DC?请求出点C的坐标;(3)如图,以AB为边在AB的下方作等边△ABP,点B在 y轴上运动时,求OP的最小值.
-
科目: 来源: 题型:
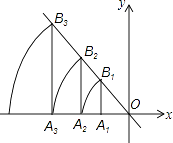
查看答案和解析>>【题目】如图:直线l:y=﹣x,点A1的坐标为(﹣1,0),过点A1作x轴的垂线交直线l于点B1 , 以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2 , 再过点A2作x轴的垂线交直线l于点B2 , 以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3…按此作法进行去,点A2016的坐标为( )
A.(﹣22016 , 0)
B.(﹣22017 , 0)
C.(﹣21008 , 0)
D.(﹣21007 , 0)
相关试题

