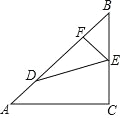
【题目】如图,△ABC中,AC=BC,∠ACB=90°,点 D,E分别在AB,BC上,且AD=BE,BD=AC,过E作EF⊥AB于F.
(1)求证:∠FED=∠CED;
(2)若 BF=![]() ,直接写出 CE的长为_______.
,直接写出 CE的长为_______.
参考答案:
【答案】(1)证明见解析;(2)5.
【解析】
(1)连接 CD,利用 SAS 定理证明△ADC≌△BED,根据全等三角形的性质得到 DC=DE,∠DCA=∠EDB,根据等角的余角相等证明;
(2)作 DH⊥EC 于 H,根据等腰三角形的性质得到 EH=HC=![]() EC,∠EDH=∠CDH,根据角平分线的性质得到 EF=EH,计算即可.
EC,∠EDH=∠CDH,根据角平分线的性质得到 EF=EH,计算即可.
解:(1)连接 CD,
∵AC=BC,∠ACB=90,
∴∠A=∠B=45°,
ADC 和△BED 中,
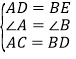
∴△ADC≌△BED(SAS),
∴DC=DE,∠DCA=∠EDB,
∴∠ECD=∠CED
∠DCA+∠ECD=∠EDB+∠FED=90°,
∴∠FED=∠ECD,
∴∠FED=∠CED;
(2)作 DH⊥EC 于 H,
∵DC=DE,DH ⊥EC,
∴EH=HC= ![]() EC,∠EDH=∠CDH,
EC,∠EDH=∠CDH,
∵DH∥AC,
∴∠CDH=∠ACD,
∴∠FDE=∠FDH,又 EF⊥AB,EH⊥DH,
∴EF=EH=![]() EC,
EC,
∵∠BFE=90°,∠B=45°,
∴EF=BF= ![]() ,
,
∴EC=5,
故答案为:5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
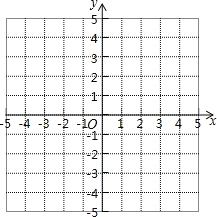
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,A(-1,5)、B(-1,0)、C(-4,3)
(1) 求出△ABC的面积
(2) 在图形中作出△ABC关于y轴的对称图形△A1B1C1,并写出A1、B1、C1的坐标
(3) 是否存在一点P到AC、AB的距离相等,同时到点A、点B的距离也相等.若存在保留作图痕迹标出点P的位置,并简要说明理由;若不存在,请说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别是C,D,E为OP上一点,则下列结论错误的是( )
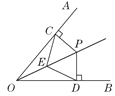
A. CE=DEB. ∠CPO=∠DEPC. ∠CEO=∠DEOD. OC=OD
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=
 x与双曲线y=
x与双曲线y= 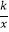 的交点A的横坐标为2
的交点A的横坐标为2
(1)求k的值
(2)如图,过点P(m,3)(m>0)作x轴的垂线交双曲线y=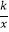 (x>0)于点M,交直线OA于点N
(x>0)于点M,交直线OA于点N 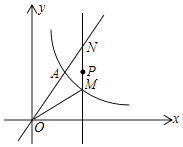
①连接OM,当OA=OM时,直接写出PN﹣PM的值
②试比较PM与PN的大小,并证明你的结论. -
科目: 来源: 题型:
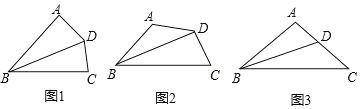
查看答案和解析>>【题目】如图,在四边形ABCD中,∠BAD=α,∠BCD=180°﹣α,BD平分∠ABC.
(1)如图,若α=90°,根据教材中一个重要性质直接可得 DA=CD,这个性质是__________.
(2)问题解决:如图,求证AD=CD;
(3)问题拓展:如图,在等腰△ABC中,∠BAC=100°,BD平分∠ABC,求证:BD+AD=BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两组邻边分别相等的四边形我们称它为筝形.如图,在四边形ABCD中,AB=AD,BC=DC,AC与BD相交于点O,下列判断正确的有_____(填序号).
①AC⊥BD;②AC,BD互相平分;③AC平分∠BCD;④∠ABC=∠ADC=90°;⑤筝形ABCD的面积为
 AC·BD.
AC·BD.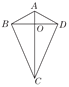
相关试题

