【题目】已知在四边形ABCD中,![]() ,
,![]() ,
,![]() .
.![]() ______
______![]() 用含x、y的代数式直接填空
用含x、y的代数式直接填空![]() ;
;![]() 如图1,若
如图1,若![]() 平分
平分![]() ,BF平分
,BF平分![]() ,请写出DE与BF的位置关系,并说明理由;
,请写出DE与BF的位置关系,并说明理由;![]() 如图2,
如图2,![]() 为四边形ABCD的
为四边形ABCD的![]() 、
、![]() 相邻的外角平分线所在直线构成的锐角.
相邻的外角平分线所在直线构成的锐角.![]() 若
若![]() ,
,![]() ,试求x、y.
,试求x、y.![]() 小明在作图时,发现
小明在作图时,发现![]() 不一定存在,请直接指出x、y满足什么条件时,
不一定存在,请直接指出x、y满足什么条件时,![]() 不存在.
不存在.

参考答案:
【答案】(1)![]() ; (2)
; (2)![]() ,理由见解析;(3) ①x=40°,y=80°;②∠DFB不存在,理由见解析.
,理由见解析;(3) ①x=40°,y=80°;②∠DFB不存在,理由见解析.
【解析】
(1)利用四边形的内角和进行计算即可;(2)由三角形外角的性质及角的平分线性质得出BF和DE的位置关系,进而作答;(3)①利用角平分线的性质以及三角形内角和定理,得出![]() ,进而得出x,y的值;②当x=y时,DC∥BF,即∠DFB=0,进而得出答案.
,进而得出x,y的值;②当x=y时,DC∥BF,即∠DFB=0,进而得出答案.
![]() ,
,![]() ,
,![]() ,
,
![]() .
.
故答案为:![]() .
.
![]() .
.
理由:如图1,
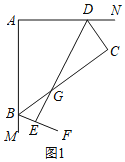
![]() 平分
平分![]() ,BF平分
,BF平分![]() ,
,
![]() ,
,![]() ,
,
又![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ;
;
![]() 由
由![]() 得:
得:![]() ,
,
![]() 、DF分别平分
、DF分别平分![]() 、
、![]() ,
,
![]() ,
,
如图2,连接DB,
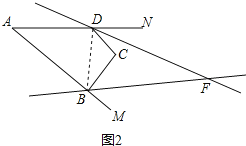
则![]() ,
,
![]() ,
,
![]() ,
,
解方程组: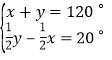 ,
,
可得:![]() ;
;
![]() 当
当![]() 时,
时,![]() ,
,
![]() 、
、![]() 相邻的外角平分线所在直线互相平行,
相邻的外角平分线所在直线互相平行,
此时,![]() 不存在.
不存在.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,
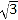 ),点C的坐标为(
),点C的坐标为( ,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )
,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )
A.
 B.
B.  C.
C.  D. 2
D. 2 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器经营业主两次购进一批同种型号的挂式空调和电风扇,第一次购进8台空调和20台电风扇;第二次购进10台空调和30台电风扇.
 若第一次用资金17400元,第二次用资金22500元,求挂式空调和电风扇每台的采购价各是多少元?
若第一次用资金17400元,第二次用资金22500元,求挂式空调和电风扇每台的采购价各是多少元? 在
在 的条件下,若该业主计划再购进这两种电器70台,而可用于购买这两种电器的资金不超过30000元,问该经营业主最多可再购进空调多少台?
的条件下,若该业主计划再购进这两种电器70台,而可用于购买这两种电器的资金不超过30000元,问该经营业主最多可再购进空调多少台? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABD中,∠A是直角,AB=3,AD=4,BC=12,DC=13,求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知等腰三角形ABC的底边BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm,求△ABC的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形OABC的边长为2,顶点A,C分别在x轴的负半轴和y轴的正半轴上,M是BC的中点,P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.
(1)求点D的坐标(用含m的代数式表示);
(2)当△APD是以AP为腰的等腰三角形时,求m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2
 =(1+
=(1+ )2,善于思考的小明进行了以下探索:
)2,善于思考的小明进行了以下探索:设a+b
 =(m+n
=(m+n )2(其中a、b、m、n均为正整数),则有a+b
)2(其中a、b、m、n均为正整数),则有a+b =m2+2n2+2mn
=m2+2n2+2mn ,
,∴a=m2+2n2,b=2mn.这样小明就找到了一种把a+b
 的式子化为平方式的方法.
的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b
 =(m+n
=(m+n )2,用含m、n的式子分别表示a、b,得:a= , b= .
)2,用含m、n的式子分别表示a、b,得:a= , b= . (2)利用所探索的结论,找一组正整数a、b、m、n填空: + = ( + )2;(答案不唯一)
(3)若a+4
 =(m+n
=(m+n )2 ,且a、m、n均为正整数,求a的值.
)2 ,且a、m、n均为正整数,求a的值.
相关试题

