搜索
【题目】小刚身高180cm，他站立在阳光下的影子长为90cm，他把手臂竖直举起，此时影子长为115cm，那么小刚的手臂超出头顶（ ）
A.35cm
B.50cm
C.25cm
D.45cm
参考答案：
【答案】B
【解析】解：设手臂竖直举起时总高度xm，则 
= 
，解得x=50cm． 故选：B．
【考点精析】掌握相似三角形的应用和平行投影是解答本题的根本，需要知道测高：测量不能到达顶部的物体的高度，通常用“在同一时刻物高与影长成比例”的原理解决；测距：测量不能到达两点间的举例，常构造相似三角形求解；太阳光线可以看成是平行光线，平行光线所形成的投影称为平行投影；作物体的平行投影：由于平行投影的光线是平行的，而物体的顶端与影子的顶端确定的直线就是光线，故根据另一物体的顶端可作出其影子．
-
科目： 来源： 题型：
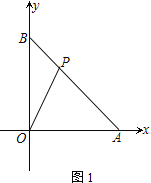
查看答案和解析>>【题目】如图1，在平面直角坐标系中，A、B坐标为(6，0)、(0，6)，P为线段AB上的一点
(1) 如图1，若S△AOP＝12，求P的坐标
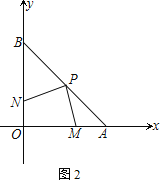
(2) 如图2，若P为AB的中点，点M、N分别是OA、OB边上的动点，点M从顶点A、点N从顶点O同时出发，且它们的速度都为1 cm/s，则在M、N运动的过程中，线段PM、PN之间有何关系？并证明
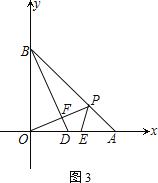
(3) 如图3，若P为线段AB上异于A、B的任意一点，过B点作BD⊥OP，交OP、OA分别与F、D两点，E为OA上一点，且∠PEA＝∠BDO，试判断线段OD与AE的数量关系，并说明理由
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，长方形纸片ABCD中，AB＝6 cm，BC＝8 cm，点E是BC边上一点，连接AE，并将△AEB沿AE折叠，得到△AEB′，以C，E，B′为顶点的三角形是直角三角形时，BE的长为____cm.
-
科目： 来源： 题型：
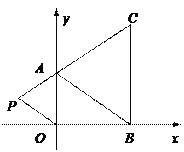
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知A，B，C三点的坐标分别为(0，a)(b，0)、(b，c)，其中a，b，c满足关系式(3a－2b)2＋
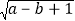＝0，|c－4|≥0．⑴求a，b，c的值；
⑵如果在第二象限内有一点P(m－1，1)，请用含m的代数式表示△AOP的面积；
⑶在⑵的条件下，m在什么范围取值时，△AOP的面积不大于△ABC的面积？请求出在符合条件的前提下、△AOP的面积最大时点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在矩形ABCD中，AB=4，BC=3，点P在AB上．若将△DAP沿DP折叠，使点A落在矩形对角线上的A′处，则AP的长为 ．
-
科目： 来源： 题型：
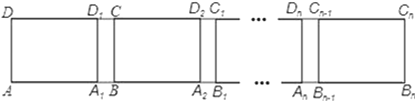
查看答案和解析>>【题目】如图，长方形ABCD中，AB=6，第一次平移长方形ABCD沿AB的方向向右平移5个单位，得到长方形A1B1C1D1，第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位，得到长方形A2B2C2D2…，第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1的方向平移5个单位，得到长方形AnBnCnDn（n＞2），若ABn的长度为56，则n=_．
-
科目： 来源： 题型：
查看答案和解析>>【题目】任何一个正整数n都可以写成两个正整数相乘的形式，对于两个因数的差的绝对值最小的一种分解a=m×n（m≤n）可称为正整数a的最佳分解，并记作F（a）=
．如：12=1×12=2×6=3×4，则F（12）= 
．则在以下结论：①F（5）=5；②F（24）=
； ③若a是一个完全平方数，则F（a）=1；
④若a是一个完全立方数，即a=x3（x是正整数），
则F（a）=x．则正确的结论有________（填序号）
相关试题
