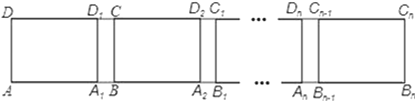
【题目】如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位,得到长方形A1B1C1D1,第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位,得到长方形A2B2C2D2…,第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1的方向平移5个单位,得到长方形AnBnCnDn(n>2),若ABn的长度为56,则n=_.
参考答案:
【答案】10
【解析】
(1)根据平移的性质得出AA1=5,A1A2=5,A2B1=A1B1﹣A1A2=6﹣5=1,进而求出AB1和AB2的长;
(2)根据(1)中所求得出数字变化规律,进而得出ABn=(n+1)×5+1求出n即可.
解:(1)∵AB=6,第1次平移将矩形ABCD沿AB的方向向右平移5个单位,得到矩形A1B1C1D1,
第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移5个单位,得到矩形A2B2C2D2…,
∴AA1=5,A1A2=5,A2B1=A1B1﹣A1A2=6﹣5=1,
∴AB1=AA1+A1A2+A2B1=5+5+1=11,
∴AB2的长为:5+5+6=16;
(2)∵AB1=2×5+1=11,AB2=3×5+1=16,
∴ABn=(n+1)×5+1=56,
解得:n=10.
“点睛”此题主要考查了平移的性质以及一元一次方程的应用,根据平移的性质得出AA1=5,A1A2=5是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A,B,C三点的坐标分别为(0,a)(b,0)、(b,c),其中a,b,c满足关系式(3a-2b)2+
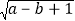 =0,|c-4|≥0.
=0,|c-4|≥0.⑴求a,b,c的值;
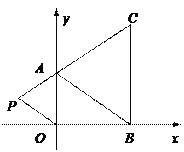
⑵如果在第二象限内有一点P(m-1,1),请用含m的代数式表示△AOP的面积;
⑶在⑵的条件下,m在什么范围取值时,△AOP的面积不大于△ABC的面积?请求出在符合条件的前提下、△AOP的面积最大时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小刚身高180cm,他站立在阳光下的影子长为90cm,他把手臂竖直举起,此时影子长为115cm,那么小刚的手臂超出头顶( )
A.35cm
B.50cm
C.25cm
D.45cm -
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=4,BC=3,点P在AB上.若将△DAP沿DP折叠,使点A落在矩形对角线上的A′处,则AP的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】任何一个正整数n都可以写成两个正整数相乘的形式,对于两个因数的差的绝对值最小的一种分解a=m×n(m≤n)可称为正整数a的最佳分解,并记作F(a)=
 .如:12=1×12=2×6=3×4,则F(12)=
.如:12=1×12=2×6=3×4,则F(12)=  .则在以下结论:
.则在以下结论:①F(5)=5;②F(24)=
 ;
; ③若a是一个完全平方数,则F(a)=1;
④若a是一个完全立方数,即a=x3(x是正整数),
则F(a)=x.则正确的结论有________(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的切线,B为切点,圆心在AC上,∠A=30°,D为
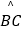 的中点.
的中点. 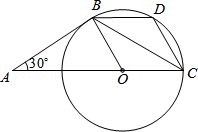
(1)求证:AB=BC;
(2)求证:四边形BOCD是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】大约1500年以前,我国古代数学家张丘建在他编写的《张丘建算经》里,曾经提出并解决了“百钱买百鸡”这个有名的数学问题,通俗地讲就是下例:
今有公鸡每只五个钱,母鸡每只三个钱,小鸡每个钱三只.用100个钱买100只鸡,问公鸡、母鸡、小鸡各买了多少只?
相关试题

