【题目】如图,长方形纸片ABCD中,AB=6 cm,BC=8 cm,点E是BC边上一点,连接AE,并将△AEB沿AE折叠,得到△AEB′,以C,E,B′为顶点的三角形是直角三角形时,BE的长为____cm.

参考答案:
【答案】3或6
【解析】试题解析:①∠B′EC=90°时,如图1,∠BEB′=90°,

由翻折的性质得∠AEB=∠AEB′=![]() ×90°=45°,
×90°=45°,
∴△ABE是等腰直角三角形,
∴BE=AB=6cm;
②∠EB′C=90°时,如图2,
由翻折的性质∠AB′E=∠B=90°,
∴A、B′、C在同一直线上,
AB′=AB,BE=B′E,
由勾股定理得,AC=![]() =10cm,
=10cm,
∴B′C=10-6=4cm,
设BE=B′E=x,则EC=8-x,
在Rt△B′EC中,B′E2+B′C2=EC2,
即x2+42=(8-x)2,
解得x=3,
即BE=3cm,
综上所述,BE的长为3或6cm.
故答案为:3或6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)、B(3,0)两点,与y轴交于点C(0,3).
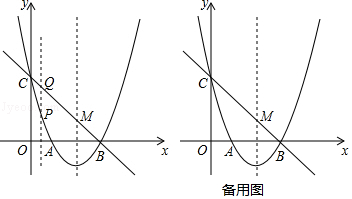
(1)求抛物线的解析式;
(2)设点P是位于直线BC下方的抛物线上一动点,过点P作y轴的平行线交直线BC于点Q,求线段PQ的最大值;
(3)在(2)的条件下,抛物线的对称轴与直线BC交于点M,问是否存在点P,使以M、P、Q为顶点的三角形与△CBO相似?若存在,请求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
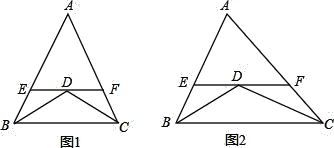
查看答案和解析>>【题目】(1)如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别交AB、AC于E、F两点,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是__________,△AEF的周长是__________;
(2)如图2,若将(1)中“△ABC中,AB=AC=10”该为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有__________个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长;
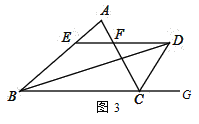
(3)已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.
-
科目: 来源: 题型:
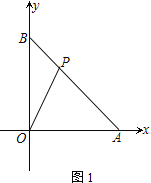
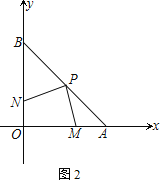
查看答案和解析>>【题目】如图1,在平面直角坐标系中,A、B坐标为(6,0)、(0,6),P为线段AB上的一点
(1) 如图1,若S△AOP=12,求P的坐标
(2) 如图2,若P为AB的中点,点M、N分别是OA、OB边上的动点,点M从顶点A、点N从顶点O同时出发,且它们的速度都为1 cm/s,则在M、N运动的过程中,线段PM、PN之间有何关系?并证明
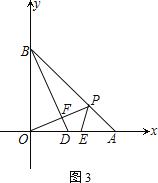
(3) 如图3,若P为线段AB上异于A、B的任意一点,过B点作BD⊥OP,交OP、OA分别与F、D两点,E为OA上一点,且∠PEA=∠BDO,试判断线段OD与AE的数量关系,并说明理由
-
科目: 来源: 题型:
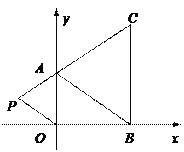
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A,B,C三点的坐标分别为(0,a)(b,0)、(b,c),其中a,b,c满足关系式(3a-2b)2+
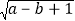 =0,|c-4|≥0.
=0,|c-4|≥0.⑴求a,b,c的值;
⑵如果在第二象限内有一点P(m-1,1),请用含m的代数式表示△AOP的面积;
⑶在⑵的条件下,m在什么范围取值时,△AOP的面积不大于△ABC的面积?请求出在符合条件的前提下、△AOP的面积最大时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小刚身高180cm,他站立在阳光下的影子长为90cm,他把手臂竖直举起,此时影子长为115cm,那么小刚的手臂超出头顶( )
A.35cm
B.50cm
C.25cm
D.45cm -
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=4,BC=3,点P在AB上.若将△DAP沿DP折叠,使点A落在矩形对角线上的A′处,则AP的长为 .
相关试题

