Question

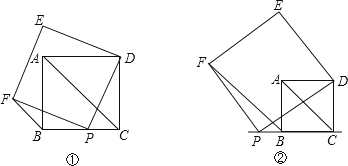
【题目】如图①，点P是正方形ABCD的BC边上的一点，以DP为边长的正方形DEFP与正方形ABCD在BC的同侧，连接AC、FB．

（1）请你判断FB与AC又怎样的位置关系？并证明你的结论；

（2）若点P在射线CB上运动时，如图②，判断（1）中的结论FB与AC的位置关系是否仍然成立？并说明理由；

（3）当点P在直线CB上运动时，请你指出点E的运动路线，不必说明理由．

Answer 1

【答案】（1）FB∥AC，证明见解析；

（2）结论仍成立，理由见解析；

（3）当点P在直线BC上移动时，E的轨迹是图中的线段GA．

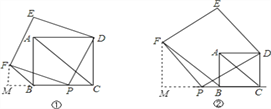
【解析】分析：（1）过F作FM⊥BC于M，证△PFM≌△DPC（AAS），推出DC=PM，FM=PC，求出∠FBM=45°即可．（2）中结论是还正确，过F作FM⊥BC于M，证△PFM≌△DPC（AAS），推出DC=PM，FM=PC，求出∠FBM=45°即可．（3）当点P在直线BC上移动时，E的轨迹是图中的线段GA，理由是△DCP绕D顺时针旋转90°，到达△DAE 即可以确定E的轨迹．

本题解析：（1）FB∥AC，

证明：过F作FM⊥BC于M，∵四边形ABCD、DEFP是正方形，∴∠ACB=45°，DC=BC，PF=DP，∠DCP=∠M=∠FPD=90°，

∴∠MFP+∠FPM=∠FPM+∠DPC=90°，∴∠MFP=∠CPD，

在△PFM和△DPC中：∠MFP＝∠DPC，∠M＝∠DCP， PF＝DP

∴△PFM≌△DPC（AAS），∵DC=PM，FM=PC，∵DC=BC，

∴BC=DC=PM，∴PM-BP=BC-BP，∴BM=CP，∵FM=CP，∴FM=BM，∵∠M=90°，

∴∠FBM=∠MFB=0.5（180°-90°）=45°，∵∠ACB=45°，∴∠ACB=∠FBM，

∴FB∥AC；

（2）结论仍成立，

理由是：过F作FM⊥BC于M，

∵四边形ABCD、DEFP是正方形，∴∠ACB=45°，DC=BC，PF=DP，∠DCP=∠M=∠FPD=90°，

∴∠MFP+∠FPM=∠FPM+∠DPC=90°，∴∠MFP=∠CPD，

在△PFM和△DPC中，

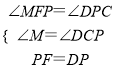，∴△PFM≌△DPC（AAS），

∵DC=PM，FM=PC，∵DC=BC，∴BC=DC=PM，∴PM+BP=BC+BP，

∴BM=CP，∵FM=CP，∴FM=BM，∵∠M=90°，

∴∠FBM=∠MFB=0.5（180°-90°）=45°，∵∠ACB=45°，∴∠ACB=∠FBM，

∴FB∥AC；

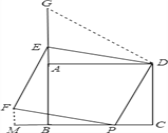
（3）当点P在直线BC上移动时，E的轨迹是图中的线段GA．