【题目】已知:在△AOB与△COD中,OA=OB,OC=OD,∠AOB=∠COD=90°.
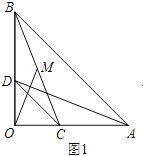
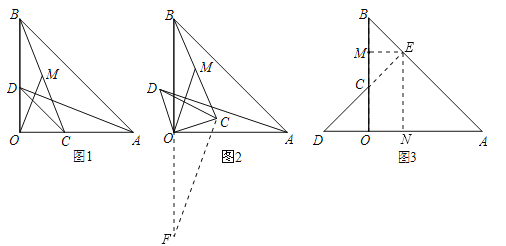
(1)如图1,点C、D分别在边OA、OB上,连结AD、BC,点M为线段BC的中点,连结OM,则请你判断线段AD与OM之间的数量关系,并加以证明.
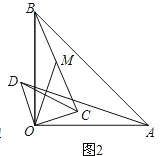
(2)如图2,将图1中的△COD绕点O逆时针旋转,旋转角为α(0°<α<90°).连结AD、BC,点M为线段BC的中点,连结OM.请你判断(1)中的结论是否仍然成立.若成立,请证明;若不成立,请说明理由;
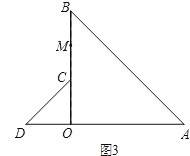
(3)如图3,将图1中的△COD绕点O逆时针旋转到使△COD的一边OD恰好与△AOB的边OA在同一条直线上时,点C落在OB上,点M为线段BC的中点.请你判断(1)中线段AD与OM之间的数量关系是否发生变化,写出你的猜想,并加以证明.
参考答案:
【答案】(1)OM=![]() ,理由见解析;(2)成立,理由见解析;(3)不变化,理由见解析
,理由见解析;(2)成立,理由见解析;(3)不变化,理由见解析
【解析】分析:(1)AD与OM之间的数量关系为AD=2OM;
(2)(1)中的结论仍然成立,理由为:如图2所示,延长BO到F,使FO=BO,连接CF,由M、O分别为BC、BF的中点,得到OM为三角形BCF的中位线,利用中位线定理得到FC=2OM,利用SAS得到三角形AOD与三角形FOC全等,利用全等三角形的对应边相等得到FC=AD,等量代换得到AD=2OM;
(3)(1)中线段AD与OM之间的数量关系没有发生变化,理由为:如图3所示,延长DC交AB于E,连结ME,过点E作EN⊥AD于N,由三角形COD与三角形AOB都为等腰直角三角形,利用等腰直角三角形的性质得到四个角为45度,进而得到三角形MCE与三角形AED为等腰直角三角形,根据EN为直角三角形ADE斜边上的中线得到AD=2EN,再利用三个角为直角的四边形为矩形得到四边形OMEN为矩形,可得出EN=OM,等量代换得到AD=2OM.
详解:(1)线段AD与OM之间的数量关系是AD=2OM;
(2)(1)的结论仍然成立,理由为:
证明:如图2,延长BO到F,使FO=BO,连结CF.
∵M为BC中点,O为BF中点,∴MO为△BCF的中位线,∴FC=2OM.
∵∠AOB=∠AOF=∠COD=90°,∴∠AOB+∠BOD=∠AOF+∠AOC,即∠AOD=∠FOC.在△AOD和△FOC中, 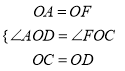 ,∴△AOD≌△FOC(SAS),∴FC=AD,∴AD=2OM.
,∴△AOD≌△FOC(SAS),∴FC=AD,∴AD=2OM.
(3)(1)中线段AD与OM之间的数量关系没有发生变化,理由为:
证明:如图3,延长DC交AB于E,连结ME,过点E作EN⊥AD于N.
∵OA=OB,OC=OD,∠AOB=∠COD=90°,∴∠A=∠D=∠B=∠BCE=∠DCO=45°,∴AE=DE,BE=CE,∠AED=90°,∴DN=AN,∴AD=2NE.
∵M为BC的中点,∴EM⊥BC,∴四边形ONEM是矩形,∴NE=OM,∴AD=2OM.
故答案为:AD=2OM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某一工程,在工程招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲工程队工程款1.2万元,乙工程队工程款0.5万元.工程领导小组根据甲、乙两队的投标书测算,有如下方案:
(1)甲队单独完成这项工程刚好如期完成;
(2)乙队单独完成这项工程要比规定日期多用6天;
(3)若甲、乙两队合作3天,余下的工程由乙队单独做也正好如期完成.
试问:(1)规定日期是多少天?
(2)在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:
①abc<0;②a(b+c)>0;③a﹣c=b;④
 .
.
其中正确的个数有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
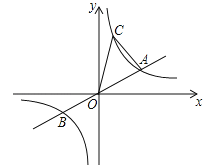
查看答案和解析>>【题目】如图,已知:直线
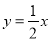 与双曲线
与双曲线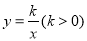 交于A.B两点,且点A的横坐标为4, 若双曲线
交于A.B两点,且点A的横坐标为4, 若双曲线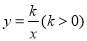 上一点C的纵坐标为8,连接AC.
上一点C的纵坐标为8,连接AC.(1)填空: k的值为_______; 点B的坐标为___________;点C的坐标为___________.
(2)直接写出关于的不等式
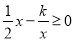 的解集.
的解集.(3)求三角形AOC的面积
(4) 若在x轴上有点M,y轴上有点N,且点M.N.A.C四点恰好构成平行四边形,直接写出点M.N的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在数轴上
 点表示数
点表示数 ,
, 点表示数
点表示数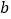 ,且
,且 、
、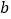 满足
满足

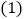 点
点 表示的数为________;点
表示的数为________;点 表示的数为________.
表示的数为________. 若点
若点 与点
与点 之间的距离表示为
之间的距离表示为 ,点
,点 与点
与点 之间的距离表示为
之间的距离表示为 ,请在数轴上找一点
,请在数轴上找一点 ,使
,使 ,则
,则 点表示的数________.
点表示的数________. 若在原点
若在原点 处放一挡板,一小球甲从点
处放一挡板,一小球甲从点 处以
处以 个单位/秒的速度向左运动;同时另一小球乙从点
个单位/秒的速度向左运动;同时另一小球乙从点 处以
处以 个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为
个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为 (秒),请分别表示出甲、乙两小球到原点的距离(用含
(秒),请分别表示出甲、乙两小球到原点的距离(用含 的代数式表示).
的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形OABC中,点B的坐标是(4,4),点E、F分别在边BC、BA上,OE=2
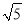 ,若∠EOF=45°,则F点的纵坐标是( )
,若∠EOF=45°,则F点的纵坐标是( )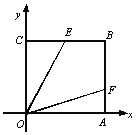
A.
 B. 1 C.
B. 1 C. 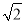 D.
D. 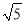 -1
-1 -
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连结菱形各边中点得到的四边形是____________ .
相关试题

