【题目】如图在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,且
,且![]() 、
、![]() 满足
满足![]()
![]()
![]() 点
点![]() 表示的数为________;点
表示的数为________;点![]() 表示的数为________.
表示的数为________.
![]() 若点
若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,请在数轴上找一点
,请在数轴上找一点![]() ,使
,使![]() ,则
,则![]() 点表示的数________.
点表示的数________.
![]() 若在原点
若在原点![]() 处放一挡板,一小球甲从点
处放一挡板,一小球甲从点![]() 处以
处以![]() 个单位/秒的速度向左运动;同时另一小球乙从点
个单位/秒的速度向左运动;同时另一小球乙从点![]() 处以
处以![]() 个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为
个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为![]() (秒),请分别表示出甲、乙两小球到原点的距离(用含
(秒),请分别表示出甲、乙两小球到原点的距离(用含![]() 的代数式表示).
的代数式表示).
参考答案:
【答案】(1)-5,7;(2)4或13;(3)当0≤t≤3.5时,小球到原点的距离为7﹣2t,当t>3.5时小球到原点的距离为2t﹣7.
【解析】
(1)根据非负数的性质列方程求出a、b的值,从而得解;
(2)根据两点间距离的表示列出绝对值方程,然后求解即可;
(3)甲小球根据数轴上的数向左减表示即可,乙小球分向左与向右移动两个部分分别列式表示即可.
(1)由题意得,a+5=0,b﹣7=0,
解得a=﹣5,b=7,
所以,点A表示﹣5,点B表示7;
(2)设点C表示x,由题意得,|﹣5﹣x|=3|7﹣x|,
所以,5+x=3(7﹣x)或5+x=﹣3(7﹣x),
解得x=4,或x=13,
所以,点C表示的数为4或13;
(3)甲:∵小球甲从点A处以1个单位/秒的速度向左运动,
∴甲到原点的距离为|﹣5﹣t|=5+t,
∵小球乙从点B处以2个单位/秒的速度也向左运动,
∴乙到达原点的时间为7÷2=3.5,
∴当0≤t≤3.5时,小球到原点的距离为7﹣2t,
当t>3.5时小球到原点的距离为2t﹣7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:
①abc<0;②a(b+c)>0;③a﹣c=b;④
 .
.
其中正确的个数有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
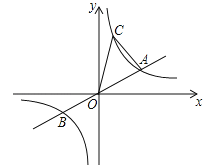
查看答案和解析>>【题目】如图,已知:直线
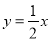 与双曲线
与双曲线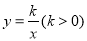 交于A.B两点,且点A的横坐标为4, 若双曲线
交于A.B两点,且点A的横坐标为4, 若双曲线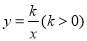 上一点C的纵坐标为8,连接AC.
上一点C的纵坐标为8,连接AC.(1)填空: k的值为_______; 点B的坐标为___________;点C的坐标为___________.
(2)直接写出关于的不等式
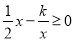 的解集.
的解集.(3)求三角形AOC的面积
(4) 若在x轴上有点M,y轴上有点N,且点M.N.A.C四点恰好构成平行四边形,直接写出点M.N的坐标.
-
科目: 来源: 题型:
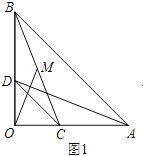
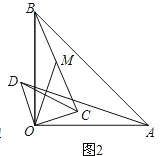
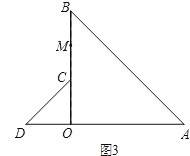
查看答案和解析>>【题目】已知:在△AOB与△COD中,OA=OB,OC=OD,∠AOB=∠COD=90°.
(1)如图1,点C、D分别在边OA、OB上,连结AD、BC,点M为线段BC的中点,连结OM,则请你判断线段AD与OM之间的数量关系,并加以证明.
(2)如图2,将图1中的△COD绕点O逆时针旋转,旋转角为α(0°<α<90°).连结AD、BC,点M为线段BC的中点,连结OM.请你判断(1)中的结论是否仍然成立.若成立,请证明;若不成立,请说明理由;
(3)如图3,将图1中的△COD绕点O逆时针旋转到使△COD的一边OD恰好与△AOB的边OA在同一条直线上时,点C落在OB上,点M为线段BC的中点.请你判断(1)中线段AD与OM之间的数量关系是否发生变化,写出你的猜想,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形OABC中,点B的坐标是(4,4),点E、F分别在边BC、BA上,OE=2
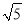 ,若∠EOF=45°,则F点的纵坐标是( )
,若∠EOF=45°,则F点的纵坐标是( )
A.
 B. 1 C.
B. 1 C. 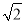 D.
D. 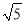 -1
-1 -
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连结菱形各边中点得到的四边形是____________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线的对称轴是直线x=2,顶点A的纵坐标为1,点B(4,0)在此抛物线上.
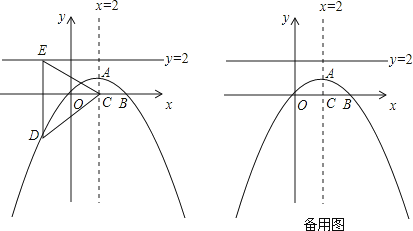
(1)求此抛物线的解析式;
(2)若此抛物线对称轴与x轴交点为C,点D(x,y)为抛物线上一动点,过点D作直线y=2的垂线,垂足为E.
①用含y的代数式表示CD2 , 并猜想CD2与DE2之间的数量关系,请给出证明;
②在此抛物线上是否存在点D,使∠EDC=120°?如果存在,请直接写出D点坐标;如果不存在,请说明理由.
相关试题

