【题目】某一工程,在工程招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲工程队工程款1.2万元,乙工程队工程款0.5万元.工程领导小组根据甲、乙两队的投标书测算,有如下方案:
(1)甲队单独完成这项工程刚好如期完成;
(2)乙队单独完成这项工程要比规定日期多用6天;
(3)若甲、乙两队合作3天,余下的工程由乙队单独做也正好如期完成.
试问:(1)规定日期是多少天?
(2)在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
参考答案:
【答案】(1)6天;(2)方案(3)最节省工程款,理由见解析
【解析】分析:(1)根据关键描述语为:“甲,乙两队合做3天,余下的工程由乙队单独做也正好如期完成”;说明甲队实际工作了3天,乙队工作了x天完成任务,工作量=工作时间×工作效率等量关系为:甲3天的工作量+乙规定日期的工作量=1列方程.
(2)再看费用情况:方案(1)、(3)不耽误工期,符合要求,可以求费用,方案(2)显然不符合要求
详解:(1)设规定日期为x天.由题意得:
![]() +
+![]() =1
=1
解得:x=6.
经检验:x=6是原方程的根.
答:规定日期为6天;
(2)显然,方案(2)不符合要求;
方案(1):1.2×6=7.2(万元);
方案(3):1.2×3+0.5×6=6.6(万元).
因为7.2>6.6,所以在不耽误工期的前提下,选方案(3)最节省工程款.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°.点D是直线BC上的一个动点,连接AD,并以AD为边在AD的右侧作等边△ADE.

(1)如图①,当点E恰好在线段BC上时,请判断线段DE和BE的数量关系,并结合图①证明你的结论;
(2)当点E不在直线BC上时,连接BE,其它条件不变,(1)中结论是否成立?若成立,请结合图②给予证明;若不成立,请直接写出新的结论;
(3)若AC=3,点D在直线BC上移动的过程中,是否存在以A、C、D、E为顶点的四边形是梯形?如果存在,直接写出线段CD的长度;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,
(1)写出数轴上点B表示的数 ;
(2)|5﹣3|表示5与3之差的绝对值,实际上也可理解为5与3两数在数轴上所对的两点之间的距离.如|x﹣3|的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离.试探索:
①:若|x﹣8|=2,则x= .
②:|x+12|+|x﹣8|的最小值为 .
(3)动点P从O点出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.求当t为多少秒时?A,P两点之间的距离为2;
(4)动点P,Q分别从O,B两点,同时出发,点P以每秒5个单位长度沿数轴向右匀速运动,Q点以P点速度的两倍,沿数轴向右匀速运动,设运动时间为t(t>0)秒.问当t为多少秒时?P,Q之间的距离为4.
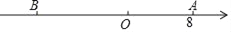
-
科目: 来源: 题型:
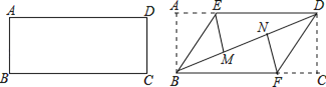
查看答案和解析>>【题目】准备一张矩形纸片,按如图操作:将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.
(1)求证:四边形BFDE是平行四边形.
(2)若四边形BFDE是菱形,BE =2,求菱形BFDE的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B、C在数轴上表示的数分别为a、b、c,且OA+OB=OC,则下列结论中:
①abc<0;②a(b+c)>0;③a﹣c=b;④
 .
.
其中正确的个数有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
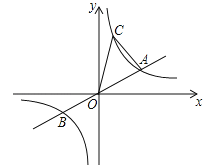
查看答案和解析>>【题目】如图,已知:直线
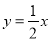 与双曲线
与双曲线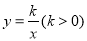 交于A.B两点,且点A的横坐标为4, 若双曲线
交于A.B两点,且点A的横坐标为4, 若双曲线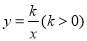 上一点C的纵坐标为8,连接AC.
上一点C的纵坐标为8,连接AC.(1)填空: k的值为_______; 点B的坐标为___________;点C的坐标为___________.
(2)直接写出关于的不等式
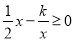 的解集.
的解集.(3)求三角形AOC的面积
(4) 若在x轴上有点M,y轴上有点N,且点M.N.A.C四点恰好构成平行四边形,直接写出点M.N的坐标.
-
科目: 来源: 题型:
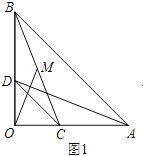
查看答案和解析>>【题目】已知:在△AOB与△COD中,OA=OB,OC=OD,∠AOB=∠COD=90°.
(1)如图1,点C、D分别在边OA、OB上,连结AD、BC,点M为线段BC的中点,连结OM,则请你判断线段AD与OM之间的数量关系,并加以证明.
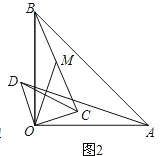
(2)如图2,将图1中的△COD绕点O逆时针旋转,旋转角为α(0°<α<90°).连结AD、BC,点M为线段BC的中点,连结OM.请你判断(1)中的结论是否仍然成立.若成立,请证明;若不成立,请说明理由;
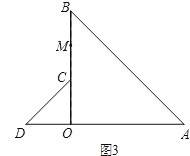
(3)如图3,将图1中的△COD绕点O逆时针旋转到使△COD的一边OD恰好与△AOB的边OA在同一条直线上时,点C落在OB上,点M为线段BC的中点.请你判断(1)中线段AD与OM之间的数量关系是否发生变化,写出你的猜想,并加以证明.
相关试题

