【题目】如图,在数轴上有A、B、C这三个点.

回答:
(1)A、B、C这三个点表示的数各是多少?
(2)A、B两点间的距离是多少?A、C两点间的距离是多少?
(3)若将点A向右移动5个单位后,则A、B、C这三个点所表示的数谁最大?
(4)应怎样移动点B的位置,使点B到点A和点C的距离相等?
参考答案:
【答案】(1)A:-6,B:1,C:4;(2)AB距离为7,AC距离为10;(3)C;(4)向左移动2个单位
【解析】
(1)直接读图即可得到;
(2)用右侧数字减左侧数字即为两点间的距离;
(3)先得出A移动后的数字,再比较着3个数字的大小;
(4)AC间的距离为10,故只需AB、BC间的距离都是5即可
(1)观察数轴得:A:-6,B:1,C:4;
(2)AB的距离为:1-(-6)=-7;
AC的距离为:4-(-6)=-10;
(3)A向右移动5个单位变为:-1
则A、B、C此刻分别为:-1、1、4,其中4最大,即点C;
(4)∵AC的距离为10
∴要使得AB、BC距离相等,则AB、BC都为5
∴只需将点B向左移动2个单位即可
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
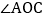 和
和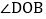 都是直角.
都是直角.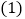 如图1,如果
如图1,如果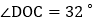 ,求
,求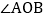 的度数;
的度数;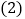 找出图1中相等的锐角,并说明相等的理由;
找出图1中相等的锐角,并说明相等的理由;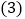 在图2中,利用三角板画一个与
在图2中,利用三角板画一个与 相等的角.
相等的角.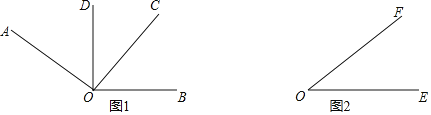
-
科目: 来源: 题型:
查看答案和解析>>【题目】网络购物越来越方便快捷,远方的朋友通过网购就可以迅速品尝到茂名的新鲜荔枝,同时也增加了种植户的收入,种植户老张去年将全部荔枝按批发价卖给水果商,收入6万元,今年的荔枝产量比去年增加2000千克,计划全部采用互联网销售,网上销售比去年的批发价高50%,若按此价格售完,今年的收入将达到10.8万元.
(1)去年的批发价和今年网上售价分别是多少?
(2)若今年老张按(1)中的网上售价销售,则每天的销量相同,20天恰好可将荔枝售完,经调查发现,当网上售价每上升0.1元/千克,每日销量将减少5千克,将网上售价定为多少,才能使日销量收入最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究
如图3,若AD=3AB,探究得: 的值为常数t,则t= .
的值为常数t,则t= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】2008年奥运会期间,一辆大巴车在一条南北方向的道路上来回运送旅客,某一天早晨该车从A地出发,晚上到达B地,预定向北为正方向,当天行驶记录如下(单位:千米)
+18,-9,+7,-14,-6,+13,-6,-8
请你根据计算回答下列问题:
(1)B地在A地何方?相距多少千米?
(2)该车这一天共行驶多少千米?
(3)若该车每千米耗油0.4升,这一天共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.

(1)求直线AB和OB的解析式.
(2)求抛物线的解析式.
(3)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.问△BOD的面积是否存在最大值?若存在,求出这个最大值并写出此时点D的坐标;若不存在说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于E交AB的延长线于点F.
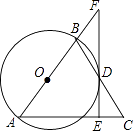
(1)求证:EF是⊙O的切线;
(2)若AE=6,FB=4,求⊙O的面积.
相关试题

