【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于E交AB的延长线于点F.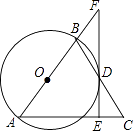
(1)求证:EF是⊙O的切线;
(2)若AE=6,FB=4,求⊙O的面积.
参考答案:
【答案】
(1)证明:连结AD、OD,如图,
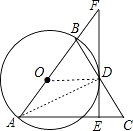
∵AB为⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵AB=AC,
∴BD=CD,
而OA=OB,
∴OD为△ABC的中位线,
∴OD∥AC,
∵EF⊥AC,
∴OD⊥EF,
∴EF是⊙O的切线
(2)解:设⊙O的半径为R,
∵OD∥AE,
∴△FOD∽△FAE,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得R=4,
∴⊙O的面积=π42=16π.
【解析】(1)连结AD、OD,根据圆周角定理可得到∠ADB=90°,即AD⊥BC,再根据等腰三角形的性质得BD=CD,则OD为△ABC的中位线,依据三角形的中位线定理可得到OD∥AC,加上EF⊥AC,于是OD⊥EF,最后,根据切线的判定定理进行证明即可;
(2)设⊙O的半径为R,利用OD∥AE得到△FOD∽△FAE,然后依据相似三角形对应边成比例可得到关于R的方程,从而可求得R的值,然后利用圆的面积公式求解即可.
【考点精析】认真审题,首先需要了解圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半),还要掌握切线的判定定理(切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有A、B、C这三个点.

回答:
(1)A、B、C这三个点表示的数各是多少?
(2)A、B两点间的距离是多少?A、C两点间的距离是多少?
(3)若将点A向右移动5个单位后,则A、B、C这三个点所表示的数谁最大?
(4)应怎样移动点B的位置,使点B到点A和点C的距离相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】2008年奥运会期间,一辆大巴车在一条南北方向的道路上来回运送旅客,某一天早晨该车从A地出发,晚上到达B地,预定向北为正方向,当天行驶记录如下(单位:千米)
+18,-9,+7,-14,-6,+13,-6,-8
请你根据计算回答下列问题:
(1)B地在A地何方?相距多少千米?
(2)该车这一天共行驶多少千米?
(3)若该车每千米耗油0.4升,这一天共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.

(1)求直线AB和OB的解析式.
(2)求抛物线的解析式.
(3)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.问△BOD的面积是否存在最大值?若存在,求出这个最大值并写出此时点D的坐标;若不存在说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.
求证:AF平分∠BAC.

【答案】证明见解析.
【解析】试题分析:先根据AB=AC,可得∠ABC=∠ACB,再由垂直,可得90°的角,在△BCE和△BCD中,利用内角和为180°,可分别求∠BCE和∠DBC,利用等量减等量差相等,可得FB=FC,再易证△ABF≌△ACF,从而证出AF平分∠BAC.
试题解析:证明:∵AB=AC(已知),
∴∠ABC=∠ACB(等边对等角).
∵BD、CE分别是高,
∴BD⊥AC,CE⊥AB(高的定义).
∴∠CEB=∠BDC=90°.
∴∠ECB=90°∠ABC,∠DBC=90°∠ACB.
∴∠ECB=∠DBC(等量代换).
∴FB=FC(等角对等边),
在△ABF和△ACF中,
 ,
,∴△ABF≌△ACF(SSS),
∴∠BAF=∠CAF(全等三角形对应角相等),
∴AF平分∠BAC.
【题型】解答题
【结束】
23【题目】如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E.

(1)求证:CD=BE;
(2)已知CD=2,求AC的长;
(3)求证:AB=AC+CD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=_____.
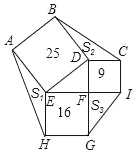
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD中,两条对角线AC,BD相交于点O,∠MON+∠BCD=180°,∠MON绕点O旋转,射线OM交边BC于点E,射线ON交边DC于点F,连接EF.
(1)如图1,当∠ABC=90°时,△OEF的形状是;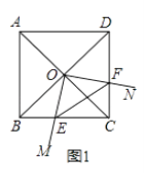
(2)如图2,当∠ABC=60°时,请判断△OEF的形状,并说明理由;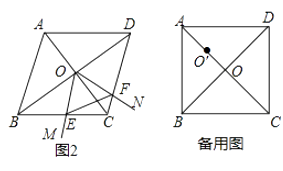
(3)在(1)的条件下,将∠MON的顶点移到AO的中点O′处,∠MO′N绕点O′旋转,仍满足∠MO′N+∠BCD=180°,射线O′M交直线BC于点E,射线O′N交直线CD于点F,当BC=4,且 =
=  时,直接写出线段CE的长.
时,直接写出线段CE的长.
相关试题

