【题目】数学活动课上,某学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究
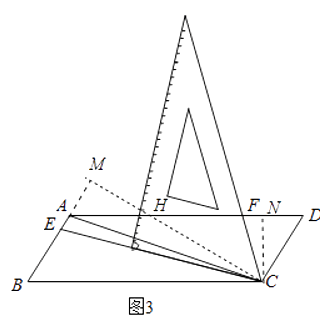
如图3,若AD=3AB,探究得: ![]() 的值为常数t,则t= .
的值为常数t,则t= . 
参考答案:
【答案】
(1)证明:①∵四边形ABCD是平行四边形,∠BAD=120°,
∴∠D=∠B=60°,
∵AD=AB,
∴△ABC,△ACD都是等边三角形,
∴∠B=∠CAD=60°,∠ACB=60°,BC=AC,
∵∠ECF=60°,
∴∠BCE+∠ACE=∠ACF+∠ACE=60°,
∴∠BCE=∠ACF,
在△BCE和△ACF中,
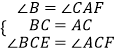
∴△BCE≌△ACF.
②∵△BCE≌△ACF,
∴BE=AF,
∴AE+AF=AE+BE=AB=AC.
(2)证明:设DH=x,由题意,CD=2x,CH= ![]() x,
x,
∴AD=2AB=4x,
∴AH=AD﹣DH=3x,
∵CH⊥AD,
∴AC= ![]() =2
=2 ![]() x,
x,
∴AC2+CD2=AD2,
∴∠ACD=90°,
∴∠BAC=∠ACD=90°,
∴∠CAD=30°,
∴∠ACH=60°,
∵∠ECF=60°,
∴∠HCF=∠ACE,
∴△ACE∽△HCF,
∴ ![]() =
= ![]() =2,
=2,
∴AE=2FH.
(3)![]()
【解析】解; (3)如图3中,作CN⊥AD于N,CM⊥BA于M,CM与AD交于点H.
∵∠ECF+∠EAF=180°,
∴∠AEC+∠AFC=180°,
∵∠AFC+∠CFN=180°,
∴∠CFN=∠AEC,∵∠M=∠CNF=90°,
∴△CFN∽△CEM,
∴ ![]() =
= ![]() ,
,
∵ABCM=ADCN,AD=3AB,
∴CM=3CN,
∴ ![]() =
= ![]() =
= ![]() ,设CN=a,FN=b,则CM=3a,EM=3b,
,设CN=a,FN=b,则CM=3a,EM=3b,
∵∠MAH=60°,∠M=90°,
∴∠AHM=∠CHN=30°,
∴HC=2a,HM=a,HN= ![]() a,
a,
∴AM= ![]() a,AH=
a,AH= ![]() a,
a,
∴AC= ![]() =
= ![]() a,
a,
AE+3AF=(EM﹣AM)+3(AH+HN﹣FN)=EM﹣AM+3AH+3HN﹣3FN=3AH+3HN﹣AM= ![]() a,
a,
∴ ![]() =
= ![]() =
= ![]() .
.
故答案为 ![]() .
.
(1)①先证明△ABC,△ACD都是等边三角形,再证明∠BCE=∠ACF即可解决问题.②根据①的结论得到BE=AF,由此即可证明.(2)设DH=x,由题意,CD=2x,CH= ![]() x,由△ACE∽△HCF,得
x,由△ACE∽△HCF,得 ![]() =
= ![]() 由此即可证明.(3)如图3中,作CN⊥AD于N,CM⊥BA于M,CM与AD交于点H.先证明△CFN∽△CEM,得
由此即可证明.(3)如图3中,作CN⊥AD于N,CM⊥BA于M,CM与AD交于点H.先证明△CFN∽△CEM,得 ![]() =
= ![]() ,由ABCM=ADCN,AD=3AB,推出CM=3CN,所以
,由ABCM=ADCN,AD=3AB,推出CM=3CN,所以 ![]() =
= ![]() =
= ![]() ,设CN=a,FN=b,则CM=3a,EM=3b,想办法求出AC,AE+3AF即可解决问题.
,设CN=a,FN=b,则CM=3a,EM=3b,想办法求出AC,AE+3AF即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为顺利通过“国家文明城市”验收,东营市政府拟对城区部分路段的人行道地砖、绿化带、排水管道等公用设施全面更新改造,根据市政建设的需要,需在40天内完成工程.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作只需10天完成.
(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)若甲工程队每天的工程费用是4.5万元,乙工程队每天的工程费用是2.5万元,请你设计一种方案,既能按时完工,又能使工程费用最少. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
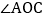 和
和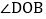 都是直角.
都是直角.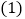 如图1,如果
如图1,如果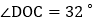 ,求
,求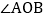 的度数;
的度数;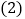 找出图1中相等的锐角,并说明相等的理由;
找出图1中相等的锐角,并说明相等的理由;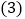 在图2中,利用三角板画一个与
在图2中,利用三角板画一个与 相等的角.
相等的角.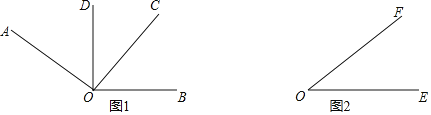
-
科目: 来源: 题型:
查看答案和解析>>【题目】网络购物越来越方便快捷,远方的朋友通过网购就可以迅速品尝到茂名的新鲜荔枝,同时也增加了种植户的收入,种植户老张去年将全部荔枝按批发价卖给水果商,收入6万元,今年的荔枝产量比去年增加2000千克,计划全部采用互联网销售,网上销售比去年的批发价高50%,若按此价格售完,今年的收入将达到10.8万元.
(1)去年的批发价和今年网上售价分别是多少?
(2)若今年老张按(1)中的网上售价销售,则每天的销量相同,20天恰好可将荔枝售完,经调查发现,当网上售价每上升0.1元/千克,每日销量将减少5千克,将网上售价定为多少,才能使日销量收入最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上有A、B、C这三个点.

回答:
(1)A、B、C这三个点表示的数各是多少?
(2)A、B两点间的距离是多少?A、C两点间的距离是多少?
(3)若将点A向右移动5个单位后,则A、B、C这三个点所表示的数谁最大?
(4)应怎样移动点B的位置,使点B到点A和点C的距离相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】2008年奥运会期间,一辆大巴车在一条南北方向的道路上来回运送旅客,某一天早晨该车从A地出发,晚上到达B地,预定向北为正方向,当天行驶记录如下(单位:千米)
+18,-9,+7,-14,-6,+13,-6,-8
请你根据计算回答下列问题:
(1)B地在A地何方?相距多少千米?
(2)该车这一天共行驶多少千米?
(3)若该车每千米耗油0.4升,这一天共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,点A的坐标为(m,m),点B的坐标为(n,﹣n),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点C.已知实数m、n(m<n)分别是方程x2﹣2x﹣3=0的两根.

(1)求直线AB和OB的解析式.
(2)求抛物线的解析式.
(3)若点P为线段OB上的一个动点(不与点O、B重合),直线PC与抛物线交于D、E两点(点D在y轴右侧),连接OD、BD.问△BOD的面积是否存在最大值?若存在,求出这个最大值并写出此时点D的坐标;若不存在说明理由.
相关试题

