【题目】如图,在△ABC中,∠B=90°,以AB为直径的⊙O交AC于D,过点D作⊙O的切线交BC于E,AE交⊙O于点F. 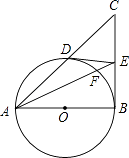
(1)求证:E是BC的中点;
(2)求证:ADAC=AEAF=4DO2 .
参考答案:
【答案】
(1)证明:连接BD,如下图所示,

∵AB是⊙O的直径,
∴BD⊥AC,
又∵∠ABC=90°,
∴CB切⊙O于点B,且ED且⊙O于点E,
∴EB=ED,
∴∠EBD=∠EDB,∠CDE+∠EDB=90°=∠EBD+∠C,
∴∠CDE=∠C,
∴ED=EC,
∴EB=EC,
即点E是BC的中点
(2)证明:∵AB=2OD,
∴AB2=4OD2,
连接BF,

由上图所示,
∵AB是⊙O的直径,
∴BF⊥AE,
∴△ABE∽△AFB,
∴ ![]() ,
,
∴AB2=AEAF,
同理可得,AB2=ADAC,
∴AB2=ADAC=AEAF,
即ADAC=AEAF=4DO2.
【解析】(1)要想证明E是BC的中点,只要证明CE=BE即可,根据已知条件可以得到DE=EC,DE=BE,从而本题得以解决;(2)根据题意可知AB=2OD,只要证明ADAC=AEAF=AB2即可,然后根据三角形相似可以证明结论成立,本题得以解决.
【考点精析】掌握切线的性质定理和相似三角形的判定与性质是解答本题的根本,需要知道切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东62°方向上,在船B的北偏西37°方向上,若AP=30海里.求船B到船P的距离PB(结果用含非特殊角的三角函数表示即可).

-
科目: 来源: 题型:
查看答案和解析>>【题目】分校为了调查初三年级学生每周的课外活动时间,随机抽查了50名初三学生,对其平均毎周参加课外活动的时间进行了调查.由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:
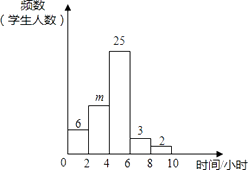
(1)求m的值;
(2)计算50名学生的课外活动时间的平均数(每组时间用其组中值表示),对初三年级全体学生平均每周的课外活动吋问做个推断;
(3)从参加课外活动时间在6~10小时的5名学生中随机选取2人,请你用列表法,求其中至少有1人课外活动时间在8~10小时的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图像分別交x轴、y轴于A、B两点.与反比例函数y=﹣
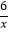 的图像交于C,D两点,DE⊥x轴于点E.已知DE=3,AE=6.
的图像交于C,D两点,DE⊥x轴于点E.已知DE=3,AE=6. 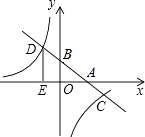
(1)求一次函数的解析式;
(2)直接写出不等式kx+b+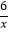 >0的解集.
>0的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,开口向下的抛物线y=ax2+bx+c交y轴于A点,交x轴于B、C两点(点B在点C的左侧).已知A点坐标为(0,﹣5),BC=4,抛物线过点(2,3).
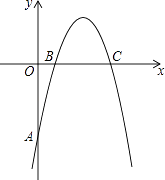
(1)求此抛物线的解析式;
(2)记抛物线的顶点为M,求△ACM的面积;
(3)在抛物线上是否存在点P,使△ACP是以AC为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列是用火柴棒拼出的一列图形.

仔细观察,找出规律,解答下列各题:
(1)第6个图中共有 根火柴;
(2)第n个图形中共有 根火柴(用含n的式子表示)
(3)第2017个图形中共有多少根火柴?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一张纸片ABCD,∠B>90°,点E是AB的中点,点G是BC上的一个动点,沿BG将纸片折叠,使点B落在纸片上的点F处,连接AF,则下列各角中与∠BEG不一定相等的是( )
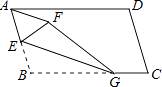
A.∠FEG
B.∠EAF
C.∠AEF
D.∠EFA
相关试题

