【题目】如图,在平面直角坐标系中,开口向下的抛物线y=ax2+bx+c交y轴于A点,交x轴于B、C两点(点B在点C的左侧).已知A点坐标为(0,﹣5),BC=4,抛物线过点(2,3).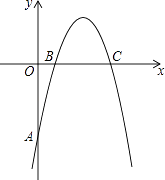
(1)求此抛物线的解析式;
(2)记抛物线的顶点为M,求△ACM的面积;
(3)在抛物线上是否存在点P,使△ACP是以AC为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:由点A的坐标为(0,﹣5)可知c=﹣5,
又∵抛物线经过点(2,3),
∴4a+2b﹣5=0①,
设B(x1,0),C(x2,0),则(x1﹣x2)2=16.即(x1+x2)2﹣2x1x2=16.
∵x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
∴ ![]() +
+ ![]() =16②.
=16②.
将方程①与方程②联立,解得:a=﹣1,b=6.
∴抛物线的解析式为y=﹣x2+6x﹣5
(2)
解:如图1所示:记AM与x轴的交点坐标为D.

∵y=﹣x2+6x﹣5=﹣(x﹣3)2+4,
∴点M的坐标为(3,4).
设直线AM的解析式为y=kx+b.
∵将A(0,﹣5)、M(3,4)代入得 ![]() ,解得:k=3,b=﹣5,
,解得:k=3,b=﹣5,
∴直线AM的解析式为y=3x﹣5.
∵令y=0得:3x﹣5=0.解得:x= ![]() ,
,
∴D( ![]() ,0).
,0).
∵令抛物线的y=0得:﹣x2+6x﹣5=0,解得x1=1,x2=5,
∴C(5,0).
∴S△ACM=S△CDA+S△CDM= ![]() ×(5﹣
×(5﹣ ![]() )×(4+5)=15
)×(4+5)=15
(3)
解:①当∠PCA=90°时,如图2所示:过点C作CP⊥AC,交抛物线与点P.
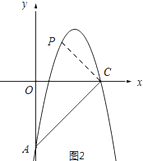
设AC的解析式为y=kx+b.
∵将点A、C的坐标代入得: ![]() ,解得:k=1,b=﹣5,
,解得:k=1,b=﹣5,
∴直线AC的解析式为y=x﹣5.
设PC的解析式为y=k1x+b1.
∵PC⊥AC,
∴k1=﹣1.
∴直线PC的解析式为y=﹣x+b1.
∵将C(5,0)代入得:﹣5+b=0,解得;b=5,
∴PC的解析式为y=﹣x+5.
∵将y=﹣x+5代入y=﹣x2+6x﹣5得:﹣x2+6x﹣5=﹣x+5,整理得:x2﹣7x+10=0,解得;x1=2,x2=5(舍去).
∴点P的坐标为(2,3)
②当∠PAC=90°时,如图3所示:
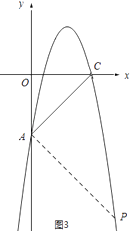
∵AP⊥AC,A(0,﹣5)
∴AP的解析式为y=﹣x﹣5.
将y=﹣x﹣5代入y=﹣x2+6x﹣5得:﹣x2+6x﹣5=﹣x﹣5,整理得:x2﹣7x=0,解得;x1=7,x2=0(舍去).
∴点P的坐标为(7,﹣12).
综上所述点P的坐标为(2,3)或(7,12)
【解析】(1)由点A的坐标可求得c的值,将(2,3)代入抛物线的解析式得到关于a、b的二元一次方程,设B(x1 , 0),C(x2 , 0),由题意可得到(x1﹣x2)2=16.结合一元二次方程根与系数的关系可得到关于a、b的另一个方程,将两个方程联立可求得a、b的值,从而得到抛物线的解析式;(2)记AM与x轴的交点坐标为D.先求得点M的坐标,从而可求得AM的解析式,然后再求得点D的坐标,最后依据S△ACM=S△CDA+S△CDM求解即可;(3)先求得AC的解析式,①当∠PCA=90°时,可求得PC的解析式,然后求得PC与抛物线的交点坐标即可;②当∠PAC=90°时,可求得PC的解析式然后求得PC与抛物线的交点坐标即可.
【考点精析】认真审题,首先需要了解二次函数的图象(二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点),还要掌握二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分校为了调查初三年级学生每周的课外活动时间,随机抽查了50名初三学生,对其平均毎周参加课外活动的时间进行了调查.由调查结果绘制了频数分布直方图,根据图中信息回答下列问题:
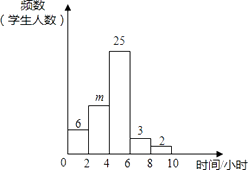
(1)求m的值;
(2)计算50名学生的课外活动时间的平均数(每组时间用其组中值表示),对初三年级全体学生平均每周的课外活动吋问做个推断;
(3)从参加课外活动时间在6~10小时的5名学生中随机选取2人,请你用列表法,求其中至少有1人课外活动时间在8~10小时的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图像分別交x轴、y轴于A、B两点.与反比例函数y=﹣
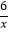 的图像交于C,D两点,DE⊥x轴于点E.已知DE=3,AE=6.
的图像交于C,D两点,DE⊥x轴于点E.已知DE=3,AE=6. 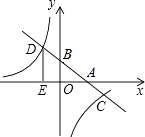
(1)求一次函数的解析式;
(2)直接写出不等式kx+b+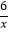 >0的解集.
>0的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=90°,以AB为直径的⊙O交AC于D,过点D作⊙O的切线交BC于E,AE交⊙O于点F.
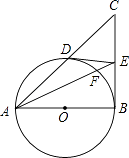
(1)求证:E是BC的中点;
(2)求证:ADAC=AEAF=4DO2 . -
科目: 来源: 题型:
查看答案和解析>>【题目】下列是用火柴棒拼出的一列图形.

仔细观察,找出规律,解答下列各题:
(1)第6个图中共有 根火柴;
(2)第n个图形中共有 根火柴(用含n的式子表示)
(3)第2017个图形中共有多少根火柴?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一张纸片ABCD,∠B>90°,点E是AB的中点,点G是BC上的一个动点,沿BG将纸片折叠,使点B落在纸片上的点F处,连接AF,则下列各角中与∠BEG不一定相等的是( )
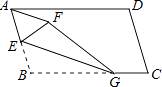
A.∠FEG
B.∠EAF
C.∠AEF
D.∠EFA -
科目: 来源: 题型:
查看答案和解析>>【题目】七
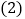 班派出
班派出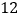 名同学参加数学竞赛,老师以
名同学参加数学竞赛,老师以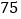 分为基准,把分数超过
分为基准,把分数超过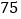 分的部分记为正数,不足部分记为负数.评分记录如下:
分的部分记为正数,不足部分记为负数.评分记录如下: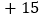 ,
, ,
,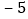 ,
,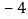 ,
,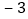 ,
,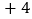 ,
,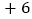 ,
,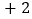 ,
,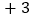 ,
,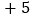 ,
,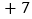 ,
,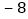 .
.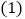 这
这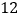 名同学中最高分和最低分各是多少?
名同学中最高分和最低分各是多少?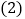 超过基准分的和低于基准分的各有多少人?
超过基准分的和低于基准分的各有多少人?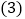 这十二名同学的平均成绩是多少?
这十二名同学的平均成绩是多少?
相关试题

