搜索
【题目】如图，已知一张纸片ABCD，∠B＞90°，点E是AB的中点，点G是BC上的一个动点，沿BG将纸片折叠，使点B落在纸片上的点F处，连接AF，则下列各角中与∠BEG不一定相等的是（ ）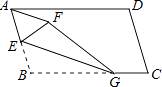 
A.∠FEG
B.∠EAF
C.∠AEF
D.∠EFA
参考答案：
【答案】C
【解析】解：由折叠的性质可知：∠BEG=∠FEG，BE=EF， 又点E是AB的中点，
∴AE=BE=EF，∠AFE=∠EAF，
又2∠BEG=∠AFE+∠EAF，
∴∠BEG=∠EAF=∠EFA，
∴∠AEF不一定与∠BEG相等，
故选C．
【考点精析】本题主要考查了平行四边形的性质和翻折变换（折叠问题）的相关知识点，需要掌握平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠B=90°，以AB为直径的⊙O交AC于D，过点D作⊙O的切线交BC于E，AE交⊙O于点F．
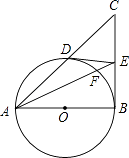
（1）求证：E是BC的中点；
（2）求证：ADAC=AEAF=4DO2 ． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，开口向下的抛物线y=ax2+bx+c交y轴于A点，交x轴于B、C两点（点B在点C的左侧）．已知A点坐标为（0，﹣5），BC=4，抛物线过点（2，3）．
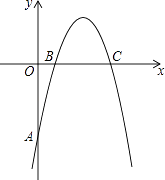
（1）求此抛物线的解析式；
（2）记抛物线的顶点为M，求△ACM的面积；
（3）在抛物线上是否存在点P，使△ACP是以AC为直角边的直角三角形？若存在，求出点P的坐标；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】下列是用火柴棒拼出的一列图形．
仔细观察，找出规律，解答下列各题：
（1）第6个图中共有 根火柴；
（2）第n个图形中共有 根火柴（用含n的式子表示）
（3）第2017个图形中共有多少根火柴？
-
科目： 来源： 题型：
查看答案和解析>>【题目】七
班派出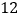
名同学参加数学竞赛，老师以
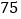分为基准，把分数超过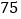分的部分记为正数，不足部分记为负数．评分记录如下：
，
，
，
，
，
，
，
，
，
，
，
．
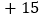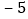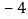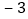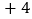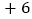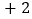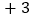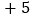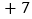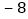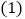这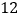名同学中最高分和最低分各是多少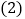？超过基准分的和低于基准分的各有多少人？
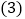这十二名同学的平均成绩是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】为喜迎祖国
周年华诞，某巡警骑摩托车在天安门前的东西大街上巡逻，某天他从天安门出发，晚上留在
处，规定向东方向为正，当天他的行驶记录如下（单位：
）：
，
，
，
，
，
，
，
．
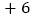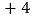处在天安门的何方？相距多少千米？
若摩托车耗油
，问这一天摩托车共耗油多少升？
在这一天中，该巡警与天安门相距最远时是多少千米？ -
科目： 来源： 题型：
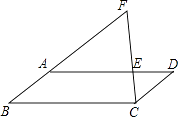
查看答案和解析>>【题目】如图，在平行四边形ABCD中，点E在AD上，连接CE并延长与BA的延长线交于点F，若AE=2ED，CD=3cm，则AF的长为（ ）
A.5cm
B.6cm
C.7cm
D.8cm
相关试题
