【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)填空:a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)]+4abc.

参考答案:
【答案】(1)a=1,b=﹣2,c=﹣3;(2)10abc,60.
【解析】
(1)先根据长方体的平面展开图确定a、b、c所对的面的数字,再根据相对的两个面上的数互为相反数,确定a、b、c的值;
(2)化简代数式后代入求值
(1)由长方体纸盒的平面展开图知,a与﹣1、b与2、c与3是相对的两个面上的数字或字母,
因为相对的两个面上的数互为相反数,
所以a=1,b=﹣2,c=﹣3.
故答案为:1,﹣2,﹣3.
(2)5a2b﹣[2a2b﹣3(2abc﹣a2b)]+4abc
=5a2b﹣(2a2b﹣6abc+3a2b)+4abc
=5a2b﹣2a2b+6abc﹣3a2b+4abc
=10abc.
当a=1,b=﹣2,c=﹣3时,
原式=10×1×(﹣2)×(﹣3)
=10×6
=60.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 已知,如图,点D是△ABC的边AB的中点,四边形BCED是平行四边形.
(1)求证:四边形ADCE是平行四边形;
(2)在△ABC中,若AC=BC,则四边形ADCE是 ;(只写结论,不需证明)
(3)在(2)的条件下,当AC⊥BC时,求证:四边形ADCE是正方形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,OA=3,OC=4
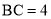 ,点B是y轴上一动点,以AC为对角线作平行四边形ABCD.
,点B是y轴上一动点,以AC为对角线作平行四边形ABCD.(1)求直线AC的函数解析式;
(2)设点
 ,记平行四边形ABCD的面积为
,记平行四边形ABCD的面积为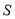 ,请写出
,请写出 与
与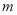 的函数关系式,并求当BD取得最小值时,函数
的函数关系式,并求当BD取得最小值时,函数 的值;
的值;(3)当点B在y轴上运动,能否使得平行四边形ABCD是菱形?若能,求出点B的坐标;若不能,说明理由.

-
科目: 来源: 题型:
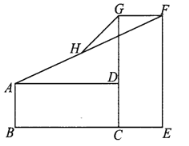
查看答案和解析>>【题目】矩形
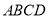 与矩形
与矩形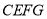 如图放置,点
如图放置,点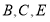 共线,
共线,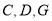 共线,连接
共线,连接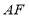 ,取
,取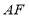 的中点
的中点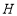 ,连接
,连接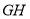 ,若
,若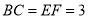 ,
,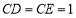 ,则
,则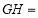 ( )
( )
A.
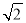 B.
B. 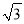 C. 2D.
C. 2D. 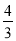
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=a(x-2)2-9经过点P(6,7),与x轴交于A、B两点,与y轴交于点C,直线AP与y轴交于点D,抛物线对称轴与x轴交于点E.
(1)求抛物线的解析式;
(2)过点E任作一条直线l(点B、C分别位于直线l的异侧),设点C到直线的距离为m,点B到直线l的距离为n,求m+n的最大值;
(3)y轴上是否存在点Q,使∠QPD=∠DEO,若存在,请求出点Q的坐标:若不存在,请说明理由.
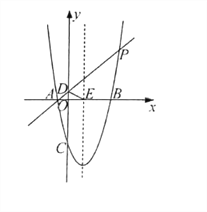
-
科目: 来源: 题型:
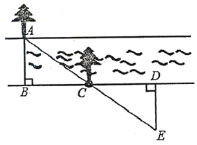
查看答案和解析>>【题目】某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
①在河流的一侧岸边B点,选对岸正对的一棵树A;
②沿河岸直走20米有一树C,继续前行20米到达D处;
③从D处沿与河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;
④测得DE的长为5米.
求河流的宽度是多少?并说明理由.
-
科目: 来源: 题型:
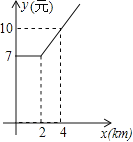
查看答案和解析>>【题目】某地出租车计费方法如图,x(km)表示行驶里程,y(元)表示车费,请根据图象解答下列问题:
(1)该地出租车的起步价是 元;
(2)当x>2时,求y与x之间的函数关系式;
(3)若某乘客有一次乘出租车的里程为18km,则这位乘客需付出租车车费多少元?
相关试题

