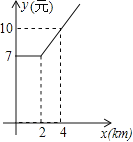
【题目】某地出租车计费方法如图,x(km)表示行驶里程,y(元)表示车费,请根据图象解答下列问题:
(1)该地出租车的起步价是 元;
(2)当x>2时,求y与x之间的函数关系式;
(3)若某乘客有一次乘出租车的里程为18km,则这位乘客需付出租车车费多少元?
参考答案:
【答案】(1)7.;(2)y=![]() x+4;(3)31.
x+4;(3)31.
【解析】
试题(1)根据函数图象可以得出出租车的起步价是7元.
(2)设当x>2时,y与x的函数关系式为y=kx+b,运用待定系数法就可以求出结论.
(3)将x=18代入(2)的解析式就可以求出y的值.
试题解析:解:(1)7.
(2)设当x>2时,y与x的函数关系式为y=kx+b,代入(2,7)、(4,10)得
![]() ,解得
,解得![]() .
.
∴y与x的函数关系式为y=![]() x+4.
x+4.
(3)把x=18代入函数关系式为y=![]() x+4得y=
x+4得y=![]() ×18+4=31.
×18+4=31.
答:这位乘客需付出租车车费31元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=﹣1,点B的坐标为(1,0),则下列结论:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正确的结论有( )个.
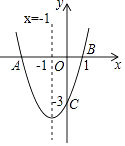
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一次函数y=kx+b(k,b都是常数,且k≠0)的图象经过点(1,0)和(0,2).
(1)当﹣2<x≤3时,求y的取值范围;
(2)已知点P(m,n)在该函数的图象上,且m﹣n=4,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,已知点A(6,0),又点B(x,y)在第一象限内,且x+y=8,设△AOB的面积是S.
(1)写出S与x之间的函数解析式,并求出x的取值范围;
(2)画出(1)中所求函数的图象.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知O为直线AB上的一点,∠COE是直角,OF平分∠AOE.
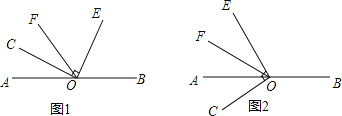
(1)如图1,若∠COF=34°,则∠BOE=______;
(2)如图1,若∠BOE=80°,则∠COF=______;
(3)若∠COF=m°,则∠BOE=______度;∠BOE与∠COF的数量关系为______.
(4)当∠COE绕点O逆时针旋转到如图2的位置时,(3)中∠BOE与∠COF的数量关系是否仍然成立?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在半径为
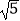 的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=4,则OP的长为( )
的⊙O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=4,则OP的长为( )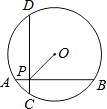
A.1
B.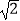
C.2
D.2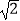
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明同学用自制的直角三角形纸板EFG测量树的高度AB,他调整自己的位置,设法使斜边EG保持水平,并且边EF所在的直线经过点A.已知纸板的两条直角边EF=60cm,FG=30cm,测得小刚与树的水平距离BD=8m,边EG离地面的高度DE=1.6m,则树的高度AB等于( )
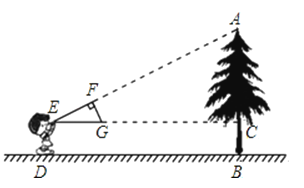
A.5m
B.5.5m
C.5.6m
D.5.8m
相关试题

