【题目】如图,在直角坐标系中,OA=3,OC=4![]() ,点B是y轴上一动点,以AC为对角线作平行四边形ABCD.
,点B是y轴上一动点,以AC为对角线作平行四边形ABCD.
(1)求直线AC的函数解析式;
(2)设点![]() ,记平行四边形ABCD的面积为
,记平行四边形ABCD的面积为![]() ,请写出
,请写出![]() 与
与![]() 的函数关系式,并求当BD取得最小值时,函数
的函数关系式,并求当BD取得最小值时,函数![]() 的值;
的值;
(3)当点B在y轴上运动,能否使得平行四边形ABCD是菱形?若能,求出点B的坐标;若不能,说明理由.

参考答案:
【答案】(1)![]() ;(2) ① 当m≤4时,S=-3m+12,② 当m>4时,S=3m-12(3) (0,
;(2) ① 当m≤4时,S=-3m+12,② 当m>4时,S=3m-12(3) (0, ![]() )
)
【解析】
试题分析:(1)根据OA、OC的长度求出A、C坐标,再利用待定系数法求解即可;
(2)根据点B的坐标可得出BC的长,结合平行四边形的面积公式求出S与m的关系式,再根据AD∥y轴即可求出当BD最短时m的值,将其代入解析式即可;
(3)根据菱形的性质找出m的值,从而根据勾股定理求解即可.
试题解析:(1)直线AC的解析式为:![]()
![]()
(2) ① 当m≤4时,S=-3m+12
② 当m>4时,S=3m-12
当BD^y轴时,BD最短为4,这时B为CO的中点,
∴m=2,S=-3×2+12=6
(3)存在
当AB=CB时,平行四边形ABCD为菱形.
∴ m2+32=(4-m)2.
解得m= ![]()
![]() .
.
∴B(0,![]()
![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】规定:二元一次方程
 有无数组解,每组解记为
有无数组解,每组解记为 ,称
,称 为亮点,将这些亮点连接得到一条直线,称这条直线是亮点的隐线,答下列问题:
为亮点,将这些亮点连接得到一条直线,称这条直线是亮点的隐线,答下列问题:(1) 已知
 ,则是隐线
,则是隐线 的亮点的是 ;
的亮点的是 ;(2) 设
 是隐线
是隐线 的两个亮点,求方程
的两个亮点,求方程 中
中 的最小的正整数解;
的最小的正整数解;(3)已知
 是实数, 且
是实数, 且 ,若
,若 是隐线
是隐线 的一个亮点,求隐线
的一个亮点,求隐线 中的最大值和最小值的和.
中的最大值和最小值的和. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面内直角坐标系中,直线y=-x+6分别于x轴、y轴交于A、B两点,点C与点A关于y轴对称,点E为线段OB上一动点(不与O、B重合),CE的延长线与AB交于点D,过A、D、E三点的圆与y轴交于点F
(1)求A、B、C三点的坐标
(2)求证:BE·EF=DE·AE
(3)若tan∠BAE=
 ,求点F的坐标
,求点F的坐标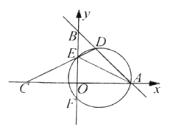
-
科目: 来源: 题型:
查看答案和解析>>【题目】 已知,如图,点D是△ABC的边AB的中点,四边形BCED是平行四边形.
(1)求证:四边形ADCE是平行四边形;
(2)在△ABC中,若AC=BC,则四边形ADCE是 ;(只写结论,不需证明)
(3)在(2)的条件下,当AC⊥BC时,求证:四边形ADCE是正方形.

-
科目: 来源: 题型:
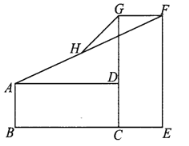
查看答案和解析>>【题目】矩形
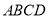 与矩形
与矩形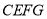 如图放置,点
如图放置,点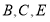 共线,
共线,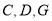 共线,连接
共线,连接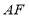 ,取
,取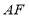 的中点
的中点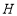 ,连接
,连接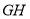 ,若
,若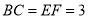 ,
,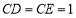 ,则
,则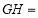 ( )
( )
A.
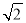 B.
B. 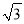 C. 2D.
C. 2D. 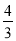
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个长方体纸盒的平面展开图,已知纸盒中相对两个面上的数互为相反数.
(1)填空:a= ,b= ,c= ;
(2)先化简,再求值:5a2b﹣[2a2b﹣3(2abc﹣a2b)]+4abc.

-
科目: 来源: 题型:
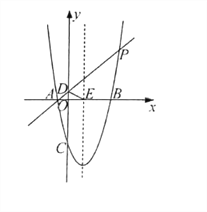
查看答案和解析>>【题目】已知抛物线y=a(x-2)2-9经过点P(6,7),与x轴交于A、B两点,与y轴交于点C,直线AP与y轴交于点D,抛物线对称轴与x轴交于点E.
(1)求抛物线的解析式;
(2)过点E任作一条直线l(点B、C分别位于直线l的异侧),设点C到直线的距离为m,点B到直线l的距离为n,求m+n的最大值;
(3)y轴上是否存在点Q,使∠QPD=∠DEO,若存在,请求出点Q的坐标:若不存在,请说明理由.
相关试题

