【题目】如图,在长方形ABCD中,AB=4cm,BE=5cm,点E是AD边上的一点,AE、DE分别长acm.bcm,满足(a-3)2+|2a+b-9|=0.动点P从B点出发,以2cm/s的速度沿B→C→D运动,最终到达点D,设运动时间为t s.
(1)a=______cm,b=______cm;
(2)t为何值时,EP把四边形BCDE的周长平分?
(3)另有一点Q从点E出发,按照E→D→C的路径运动,且速度为1cm/s,若P、Q两点同时出发,当其中一点到达终点时,另一点随之停止运动.求t为何值时,△BPQ的面积等于6cm2.


参考答案:
【答案】(1)3,3;(2)t=2s;(3)t=![]() s或
s或![]() s或5s.
s或5s.
【解析】
(1)根据非负数的性质即可求出a,b的值;
(2)计算出四边形BCDE的周长,根据ED+DC=7<9判断出点P在BC上,从而得到BP的值,进而根据点P的速度求出时间即可;
(3)分别对点P和点Q的位置进行分类讨论,①当0<t≤3,②当3<t≤![]() ,③当
,③当![]() <t≤5,表达出△BPQ的面积,列出方程即可解答.
<t≤5,表达出△BPQ的面积,列出方程即可解答.
解:(1)∵(a-3)2+|2a+b-9|=0,
∴a-3=0,2a+b-9,
解得:a=3,b=3,
故答案为:3,3.
(2)C四边形BCDE=BC+CD+DE+EB=18cm
若EP把四边形BCDE的周长平分,
∵ED+DC=7<9,
∴点P在BC上,
则BE+BP=9cm,
BP=4cm,
∴t=![]() =2s,
=2s,
∴当t为2s时,EP把四边形BCDE的周长平分.
(3)∵BC=6,ED=3,DC=4,
∴当点P与点Q相遇时,2t+t=6+3+4,解得:t=![]() s,
s,
当t=3时,点P到达点C,点Q到达点D,
当t=5时,点P到达点D,两点运动停止,
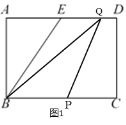
①当0<t≤3,点P在BC上,此时点Q在线段ED上,如图1,
则![]() ,
,
解得:t=![]() s,
s,
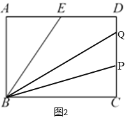
②当3<t≤![]() ,相遇前,此时点P,点Q均在CD上,如图2,
,相遇前,此时点P,点Q均在CD上,如图2,
则PC=2t-6,CQ=3+4-t,
∴PQ=3+4-t-(2t-6)
![]()
解得:t=![]() s,
s,
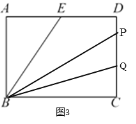
③当![]() <t≤5,相遇后,点P,点Q均在CD上,如图3,
<t≤5,相遇后,点P,点Q均在CD上,如图3,
则PQ=PC-CQ=2t-6-(7-t)=3t-13,
∴![]()
解得:t=5s
∴综上,t=![]() s或
s或![]() s或5s.
s或5s.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,∠MON=80°,点A、B分别在射线OM、ON上移动,△AOB的角平分线AC与BD交于点P.试问:随着点A、B位置的变化,∠APB的大小是否会变化?若保持不变,请求出∠APB的度数;若发生变化,求出变化范围.

(2)两条相交的直线OX、OY,使∠XOY=n,在射线OX、OY上分别再任意取A、B两点,作∠ABY的平分线BD,BD的反向延长线交∠OAB的平分线于点C,随着点A、B位置的变化,∠C的大小是否会变化?若保持不变,请求出∠C的度数;若发生变化,求出变化范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分)已知:如图,△ABC中,D是AB的中点,E是AC上一点,EF∥AB,DF∥BE.
(1)猜想:DF与AE的关系是______.
(2)试说明你猜想的正确性.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,下列结论:
①若通话时间少于120分,则A方案比B方案便宜20元;
②若通话时间超过200分,则B方案比A方案便宜12元;
③若通讯费用为60元,则B方案比A方案的通话时间多;
④若两种方案通讯费用相差10元,则通话时间是145分或185分.其中正确结论的序号是 .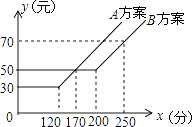
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,E、F分别在AD、BC边上,且AE=CF.
求证:(1)△ABE≌△CDF;
(2)四边形BFDE是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AB=15,AC=13,AD⊥BC于D,AD=12,⊙O是△ABC的外接圆,则⊙O的半径是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,已知AD=10,CD=4,B′D=2.
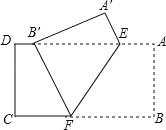
(1)求证:B′E=BF;
(2)求AE的长.
相关试题

