【题目】函数f(x)= ![]() +a(x﹣1)﹣2.
+a(x﹣1)﹣2.
(1)当a=0时,求函数f(x)的极值;
(2)若对任意x∈(0,1)∪(1,+∞),不等式 ![]() <
< ![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
参考答案:
【答案】
(1)解:当a=0时,f(x)= ![]() ﹣2.x>0,
﹣2.x>0,
∴f′(x)= ![]()
令f′(x)=0,解得x= ![]() ,
,
当f′(x)>0时,即0<x< ![]() ,函数单调递增,
,函数单调递增,
当f′(x)<0时,即x> ![]() ,函数单调递减,
,函数单调递减,
∴当x= ![]() 时,函数f(x)有极大值,极大值为f(
时,函数f(x)有极大值,极大值为f( ![]() )=e﹣2,无极小值;
)=e﹣2,无极小值;
(2)解:原不等式等价于 ![]() +
+ ![]() >0,即
>0,即 ![]() >0,
>0,
∴ ![]() [lnx+a(x2﹣1)﹣2(x﹣1)]>0,
[lnx+a(x2﹣1)﹣2(x﹣1)]>0,
令g(x)=lnx+a(x2﹣1)﹣2(x﹣1),g(1)=0,
∴g′(x)= ![]() +2ax﹣2=
+2ax﹣2= ![]() ,
,
∵ ![]() [lnx+a(x2﹣1)﹣2(x﹣1)]>0,
[lnx+a(x2﹣1)﹣2(x﹣1)]>0,
g(2)=ln2+3a﹣2>0a> ![]() >0,
>0,
①当a≥ ![]() 时,2ax2﹣2x+1≥x2﹣2x+1≥(x﹣1)2>0,
时,2ax2﹣2x+1≥x2﹣2x+1≥(x﹣1)2>0,
∴g′(x)>0,
∴g(x)在(0,+∞)上单调递增,
∴x∈(0,1),g(x)<0,x∈(1,+∞),g(x)>0,
∴ ![]() g(x)>0,
g(x)>0,
②当0<a< ![]() 时,令2ax2﹣2x+1=0,解得x=
时,令2ax2﹣2x+1=0,解得x= ![]() >1,
>1,
∴x∈(1, ![]() )时,g′(x)<0,函数g(x)单调递减,
)时,g′(x)<0,函数g(x)单调递减,
∴g(x)<g(1)=0,
∴ ![]() g(x)<0,不合题意,舍去,
g(x)<0,不合题意,舍去,
综上所述a≥ ![]()
【解析】(1)先求导,根据导数和函数的极值的关系即可求出,(2)原不等式等价于 ![]() +
+ >0,即
![]() >0,构造函数g(x)=lnx+a(x2﹣1)﹣2(x﹣1),根据导数和函数的最值得关系,分类讨论即可证明
>0,构造函数g(x)=lnx+a(x2﹣1)﹣2(x﹣1),根据导数和函数的最值得关系,分类讨论即可证明
【考点精析】本题主要考查了函数的极值与导数的相关知识点,需要掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能正确解答此题.
是极小值才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在以A、B、C、D、E为顶点的五面体中,AD⊥平面ABC,AD∥BE,AC⊥CB,AB=2BE=4AD=4.

(1)O为AB的中点,F是线段BE上的一点,BE=4BF,证明:OF∥平面CDE;
(2)当直线DE与平面CBE所成角的正切值为 时,求平面CDE与平面ABC所成锐二面角的余弦值.
时,求平面CDE与平面ABC所成锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】2017年是某市大力推进居民生活垃圾分类的关键一年,有关部门为宣传垃圾分类知识,面向该市市民进行了一次“垃圾分类知识”的网络问卷调查,每位市民仅有一次参与机会,通过抽样,得到参与问卷调查中的1000人的得分数据,其频率分布直方图如图所示:

(1)由频率分布直方图可以认为,此次问卷调查的得分Z服从正态分布N(μ,210),μ近似为这1000人得分的平均值(同一组数据用该区间的中点值作代表),利用该正态分布,求P(50.5<Z<94).
(2)在(1)的条件下,有关部门为此次参加问卷调查的市民制定如下奖励方案: ①得分不低于μ可获赠2次随机话费,得分低于μ则只有1次;
②每次赠送的随机话费和对应概率如下:赠送话费(单位:元)
10
20
概率


现有一位市民要参加此次问卷调查,记X(单位:元)为该市民参加问卷调查获赠的话费,求X的分布列.
附: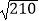 ≈14.5
≈14.5
若Z~N(μ,δ2),则P(μ﹣δ<Z<μ+δ)=0.6826,P(μ﹣2δ<Z<μ+2δ)=0.9544. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,△ABC的周长为12,AB,AC边的中点分别为F1(﹣1,0)和F2(1,0),点M为BC边的中点.
(1)求点M的轨迹方程;
(2)设点M的轨迹为曲线T,直线MF1与曲线T另一个交点为N,线段MF2中点为E,记S=S +S
+S  ,求S的最大值.
,求S的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,直线l的参数方程为
 (t为参数),其中0≤α<π.在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C1:ρ=4cosθ.直线l与曲线C1相切.
(t为参数),其中0≤α<π.在以O为极点,x轴的正半轴为极轴的极坐标系中,曲线C1:ρ=4cosθ.直线l与曲线C1相切.
(1)将曲线C1的极坐标方程化为直角坐标方程,并求α的值.
(2)已知点Q(2,0),直线l与曲线C2:x2+ =1交于A,B两点,求△ABQ的面积.
=1交于A,B两点,求△ABQ的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣3,﹣1,
 ,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组
,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组  无解,且使关于x的分式方程
无解,且使关于x的分式方程  ﹣
﹣  =﹣1有整数解,那么这5个数中所有满足条件的a的值之和是( )
=﹣1有整数解,那么这5个数中所有满足条件的a的值之和是( )
A.﹣3
B.﹣2
C.﹣
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】穿越青海境内的兰新高铁极大地改善了沿线人民的经济文化生活,该铁路沿线甲,乙两城市相距480km,乘坐高铁列车比乘坐普通快车能提前4h到达,已知高铁列车的平均行驶速度比普通列车快160km/h,设普通列车的平均行驶速度为xkm/h,依题意,下面所列方程正确的是( )
A. ﹣
﹣  =4
=4
B. =4
=4
C.
 =4
=4
D.
 =4
=4
相关试题

