【题目】从﹣3,﹣1, ![]() ,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组
,1,3这五个数中,随机抽取一个数,记为a,若数a使关于x的不等式组  无解,且使关于x的分式方程
无解,且使关于x的分式方程 ![]() ﹣
﹣ ![]() =﹣1有整数解,那么这5个数中所有满足条件的a的值之和是( )
=﹣1有整数解,那么这5个数中所有满足条件的a的值之和是( )
A.﹣3
B.﹣2
C.﹣ ![]()
D.![]()
参考答案:
【答案】A
【解析】解:解  得
得 ![]() ,
,
∵不等式组  无解,
无解,
∴a≤1,
解方程 ![]() ﹣
﹣ ![]() =﹣1得x=
=﹣1得x= ![]() ,
,
∵x= ![]() 为整数,a≤1,
为整数,a≤1,
∴a=﹣3,-1,1
∴所有满足条件的a的值之和是﹣3+(-1)+1=-3,
故选A.
【考点精析】解答此题的关键在于理解去分母法的相关知识,掌握先约后乘公分母,整式方程转化出.特殊情况可换元,去掉分母是出路.求得解后要验根,原留增舍别含糊,以及对一元一次不等式组的解法的理解,了解解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是等腰直角三角形,∠BAC=90°,CD=
 BC,DE⊥CE,DE=CE,连接AE,点M是AE的中点.
BC,DE⊥CE,DE=CE,连接AE,点M是AE的中点. 
(1)如图1,若点D在BC边上,连接CM,当AB=4时,求CM的长;
(2)如图2,若点D在△ABC的内部,连接BD,点N是BD中点,连接MN,NE,求证:MN⊥AE;
(3)如图3,将图2中的△CDE绕点C逆时针旋转,使∠BCD=30°,连接BD,点N是BD中点,连接MN,探索 的值并直接写出结果.
的值并直接写出结果. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,二次函数y=
 x2﹣2x+1的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.
x2﹣2x+1的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48. 
(1)求直线AB和直线BC的解析式;
(2)点P是线段AB上一点,点D是线段BC上一点,PD∥x轴,射线PD与抛物线交于点G,过点P作PE⊥x轴于点E,PF⊥BC于点F.当PF与PE的乘积最大时,在线段AB上找一点H(不与点A,点B重合),使GH+ BH的值最小,求点H的坐标和GH+
BH的值最小,求点H的坐标和GH+  BH的最小值;
BH的最小值;
(3)如图2,直线AB上有一点K(3,4),将二次函数y= x2﹣2x+1沿直线BC平移,平移的距离是t(t≥0),平移后抛物线上点A,点C的对应点分别为点A′,点C′;当△A′C′K′是直角三角形时,求t的值.
x2﹣2x+1沿直线BC平移,平移的距离是t(t≥0),平移后抛物线上点A,点C的对应点分别为点A′,点C′;当△A′C′K′是直角三角形时,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)( )
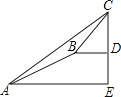
A.8.1米
B.17.2米
C.19.7米
D.25.5米 -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在直线道路上同起点、同终点、同方向,分别以不同的速度匀速跑步1500米,先到终点的人原地休息,已知甲先出发30秒后,乙才出发,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示,则乙到终点时,甲距终点的距离是米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD中,对角线AC,BD相交于点O,DE平分∠ADO交AC于点E,把△ADE沿AD翻折,得到△ADE′,点F是DE的中点,连接AF,BF,E′F.若AE=
 .则四边形ABFE′的面积是 .
.则四边形ABFE′的面积是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】为响应“全民阅读”号召,某校在七年级800名学生中随机抽取100名学生,对概念机学生在2015年全年阅读中外名著的情况进行调查,整理调查结果发现,学生阅读中外名著的本数,最少的有5本,最多的有8本,并根据调查结果绘制了如图所示的不完整的条形统计图,其中阅读了6本的人数占被调查人数的30%,根据图中提供的信息,补全条形统计图并估计该校七年级全体学生在2015年全年阅读中外名著的总本数.

相关试题

