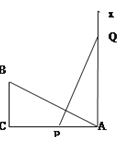
【题目】如图,∠C=90°,AC=8,BC=3,线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到AP=_________时,才能使ΔABC与ΔAPQ 全等。
参考答案:
【答案】8或3;
【解析】
由题意要分情况讨论:①当P与C重合时,AC=AP=8时,△BCA≌△QAP;②当AP=BC=3时,△BCA≌△PAQ.
①当P与C重合时,AC=AP=8时,△BCA≌△QAP,
在Rt△BCA和Rt△QAC中,
PQ=AB,
AC=AP,
∴Rt△BCA≌Rt△QAC(HL);
②当AP=BC=3时,△BCA≌△PAQ,
在Rt△BCA和Rt△QAC中,
QP=AB,
BC=AP,
∴Rt△BCA≌Rt△PAQ(HL);
故答案为:8或3.
-
科目: 来源: 题型:
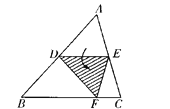
查看答案和解析>>【题目】如图,点D为边AB的中点,DE∥BC,将△ABC沿线段DE折叠,使点A落在点F处,若∠B=50°,则∠EDF=_______,∠BDF=_______,若AB=10cm,则FD= ________cm。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线C1:y=ax2+4x+4a(0<a<2)

(1)当C1与x轴有唯一一个交点时,求此时C1的解析式;
(2)如图①,若A(1,yA),B(0,yB),C(﹣1,yC)三点均在C1上,连BC作AE∥BC交抛物线C1于E,求点E到y轴的距离;
(3)若a=1,将抛物线C1先向右平移3个单位,再向下平移2个单位得到抛物线C2 , 如图②,抛物线C2与x轴相交于点M、N(M点在N点的左边),抛物线的对称轴交x轴于点F,过点F的直线l与抛物线C2相交于P,Q(P在第四象限)且S△FMQ=2S△FNP , 求直线l的解析式. -
科目: 来源: 题型:
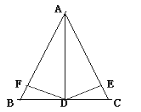
查看答案和解析>>【题目】如图:在△ABC中,AD是∠BAC的平分线,DE⊥AC于E,DF⊥AB于F,且FB=CE,则下列结论:①DE=DF,②AE=AF,③BD=CD,④AD⊥BC。
其中正确的有___________ (填序号)。
-
科目: 来源: 题型:
查看答案和解析>>【题目】作图题
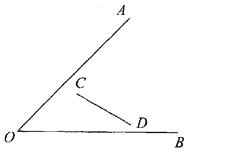
(1)如图:已知∠AOB和线段CD,求作一点P,使PC=PD,并且点P到∠AOB的两边距离相等(尺规作图,不写作法,保留作图痕迹,写出结论);
(2)如图:在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
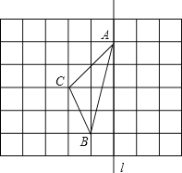
①在图中画出与关于直线
 成轴对称的△A′B′C′;
成轴对称的△A′B′C′;②线段CC′被直线
 _________;
_________;③△ABC的面积为_________;
④在直线
 上找一点P,使PB+PC的长最短.
上找一点P,使PB+PC的长最短. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,将正方形的边AD绕点A顺时针旋转到AE,连接BE、DE,过点A作AF⊥BE于F,交直线DE于P.
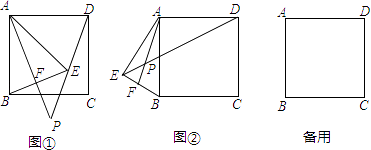
(1)如图①,若∠DAE=40°,求∠P的度数;
(2)如图②,若90°<∠DAE<180°,其它条件不变,试探究线段AP、DP、EP之间的数量关系,并说明理由;
(3)继续旋转线段AD,若旋转角180°<∠DAE<270°,则线段AP、DP、EP之间的数量关系为(直接写出结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ACB=90°,AC=BC,BD⊥DE,AE⊥DE,垂足分别为D、E.(这几何模型具备“一线三直角”)如下图:
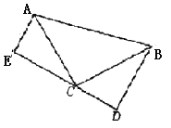
(1)①请你证明:△ACE≌△CBD;②若AE=3,BD=5,求DE的长;
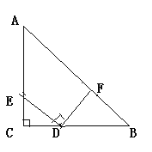
(2)迁移:如图:在等腰Rt△ABC中,且∠C=90°,CD=2,BD=3,D、E分别是边BC,AC上的点,将DE绕点D顺时针旋转90°,点E刚好落在边AB上的点F处,则CE=________。(不要求写过程)
相关试题

