搜索
【题目】作图题
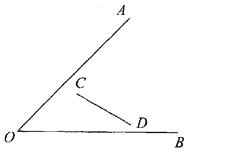
（1）如图：已知∠AOB和线段CD，求作一点P，使PC=PD，并且点P到∠AOB的两边距离相等(尺规作图，不写作法，保留作图痕迹，写出结论)；
（2）如图：在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．
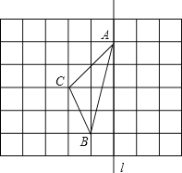
①在图中画出与关于直线
成轴对称的△A′B′C′；
②线段CC′被直线_________；
③△ABC的面积为_________；
④在直线上找一点P，使PB+PC的长最短．
参考答案：
【答案】（1）见解析；（2）①见解析；②垂直平分；③
.
【解析】
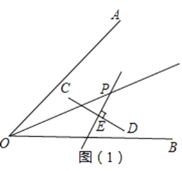
（1）如图（1）：根据分析得OP为∠AOB的角平分线，PE是线段CD的垂直平分线。
（2）
①如图所示：
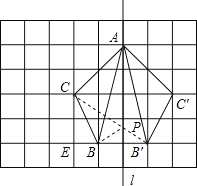
②∵△ABC与△AB′C′关于直线l成轴对称，
∴线段CC′被直线l垂直平分；
故答案为：垂直平分；
③连接B′C，交直线l与点P，此时PB+PC的长最短，
可得BP=B′P，
则B′C=BP+CP=
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中，抛物线C1：y=ax2+4x+4a（0＜a＜2）
（1）当C1与x轴有唯一一个交点时，求此时C1的解析式；
（2）如图①，若A（1，yA），B（0，yB），C（﹣1，yC）三点均在C1上，连BC作AE∥BC交抛物线C1于E，求点E到y轴的距离；
（3）若a=1，将抛物线C1先向右平移3个单位，再向下平移2个单位得到抛物线C2 ， 如图②，抛物线C2与x轴相交于点M、N（M点在N点的左边），抛物线的对称轴交x轴于点F，过点F的直线l与抛物线C2相交于P，Q（P在第四象限）且S△FMQ=2S△FNP ， 求直线l的解析式． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图：在△ABC中，AD是∠BAC的平分线，DE⊥AC于E，DF⊥AB于F，且FB=CE，则下列结论：①DE=DF，②AE=AF，③BD=CD，④AD⊥BC。
其中正确的有___________ (填序号)。
-
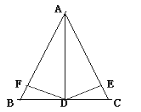
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠C=90°，AC=8，BC=3，线段PQ=AB，P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动，问P点运动到AP=_________时，才能使ΔABC与ΔAPQ 全等。
-
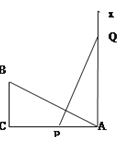
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，将正方形的边AD绕点A顺时针旋转到AE，连接BE、DE，过点A作AF⊥BE于F，交直线DE于P．
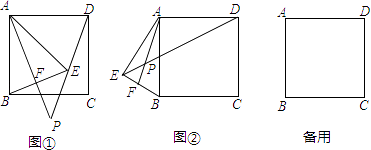
（1）如图①，若∠DAE=40°，求∠P的度数；
（2）如图②，若90°＜∠DAE＜180°，其它条件不变，试探究线段AP、DP、EP之间的数量关系，并说明理由；
（3）继续旋转线段AD，若旋转角180°＜∠DAE＜270°，则线段AP、DP、EP之间的数量关系为（直接写出结果） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知∠ACB＝90°，AC＝BC，BD⊥DE，AE⊥DE，垂足分别为D、E．(这几何模型具备“一线三直角”）如下图：
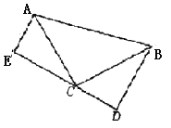
(1)①请你证明：△ACE≌△CBD；②若AE＝3，BD＝5，求DE的长;
（2）迁移：如图：在等腰Rt△ABC中，且∠C=90°，CD=2，BD=3，D、E分别是边BC，AC上的点，将DE绕点D顺时针旋转90°，点E刚好落在边AB上的点F处，则CE=________。（不要求写过程）
-
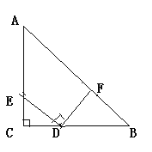
科目： 来源： 题型：
查看答案和解析>>【题目】如图①：在四边形ABCD中，AB=AD，∠BAD=120°，∠B=ADC=90°，E、F分别是BC，CD上的点，且∠EAF=60°，探究图中线段BE，EF，FD之间的数量关系。
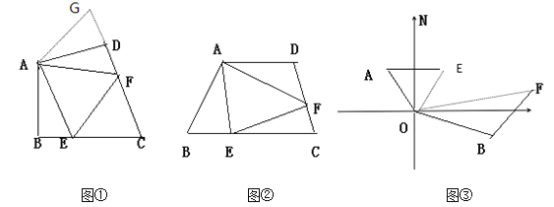
（1）小王同学探究此问题的方法是：延长FD到点G，使DG=BE，连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，即可得出BE，EF，FD之间的数量关系，他的结论应是____________。
象上面这样有公共顶点，锐角等于较大角的一半，且组成这个较大角的两边相等的几何模型称为半角模型。
（2）拓展 如图②，若在四边形ABCD中,，AB=AD，∠B+∠D=180°，E、F分别是BC，CD上的点，且∠EAF=
∠BAD，则BE，EF，FD之间的数量关系是________________。请证明你的结论。
（3）实际应用 如图③,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西35°的A处，舰艇乙在指挥中心南偏东75°的B处,，且两舰艇到指挥中心的距离相等接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里小时的速度前进，1.2小时后,指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为65°,试求此时两舰艇之间的距离是_____________海里 (直接写出答案）。
相关试题
