【题目】在平面直角坐标系中,抛物线C1:y=ax2+4x+4a(0<a<2)
(1)当C1与x轴有唯一一个交点时,求此时C1的解析式;
(2)如图①,若A(1,yA),B(0,yB),C(﹣1,yC)三点均在C1上,连BC作AE∥BC交抛物线C1于E,求点E到y轴的距离;
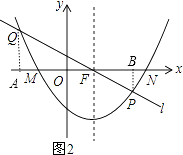
(3)若a=1,将抛物线C1先向右平移3个单位,再向下平移2个单位得到抛物线C2 , 如图②,抛物线C2与x轴相交于点M、N(M点在N点的左边),抛物线的对称轴交x轴于点F,过点F的直线l与抛物线C2相交于P,Q(P在第四象限)且S△FMQ=2S△FNP , 求直线l的解析式.
参考答案:
【答案】
(1)
解:根据题意得△=42﹣4a4a=0,解得a1=1,a2=﹣1,
而0<a<2,
所以a=1,
所以此时C1的解析式为y=x2+4x+4;
(2)
解:根据题意得A(1,5a+4),B(0,4a),C(﹣1,5a﹣4),
设直线BC的解析式为y=kx+4a,
把C(﹣1,5a﹣4)代入得﹣k+4a=5a﹣4,解得k=4﹣a,
∴直线BC的解析式为y=(4﹣a)x+4a,
∵BC∥AE,
∴AE的解析式可设为y=(4﹣a)x+n,
把A(1,5a+4)代入得4﹣a+n=5a+4,解得n=6a,
∴直线AE的解析式为y=(4﹣a)x+6a,
方程组 ![]() 消去y得x2+x﹣2=0,解得x1=1,x2=﹣2,
消去y得x2+x﹣2=0,解得x1=1,x2=﹣2,
∴E点的横坐标为﹣2,
∴点E到y轴的距离为2;
(3)
解:作QA⊥x轴于A,PB⊥x轴于B,如图,
当a=1时,y=x2+4x+4=(x+2)2,抛物线C1的顶点坐标为(﹣2,0),把点(﹣2,0)先向右平移3个单位,再向下平移2个单位得到对应点的坐标为(1,﹣2),
所以抛物线C2的解析式为y=(x﹣1)2﹣2,即y=x2﹣2x﹣1,则抛物线的对称轴为直线x=1,所以F(1,0)
∵抛物线C2与x轴相交于点M、N(M点在N点的左边),
∴FM=FN,
∵S△FMQ=2S△FNP,
∴QA=2PB,
∵AQ∥PB,
∴ ![]() =2,即FA=2BF,
=2,即FA=2BF,
设P(t,t2﹣2t﹣1),则BF=t﹣1,
∴AF=2(t﹣1),
∴OA=2(t﹣1)﹣1=2t﹣3,
∴Q[3﹣2t,(3﹣2t)2﹣2(3﹣2t)﹣1]
∴(3﹣2t)2﹣2(3﹣2t)﹣1=﹣2(t2﹣2t﹣1),
整理得t2﹣2t=0,解得t1=0(舍去),t2=2,
∴P(2,﹣1),Q(﹣1,2),
设直线PQ的解析式为y=px+q,
把P(2,﹣1),Q(﹣1,2)代入得 ![]() ,解得
,解得 ![]() ,
,
∴直线l的解析式为y=﹣x+1.
【解析】(1)根据△的意义和抛物线与x轴的交点问题得△=42﹣4a4a=0,然后解方程求出满足条件的a的值,从而得到此时C1的解析式;(2)先用a表示出A(1,5a+4),B(0,4a),C(﹣1,5a﹣4),再利用待定系数法得到直线BC的解析式为y=(4﹣a)x+4a,根据两直线平行问题,AE的解析式可设为y=(4﹣a)x+n,则把A(1,5a+4)代入得n=6a,所以直线AE的解析式为y=(4﹣a)x+6a,通过解方程组 ![]() 可得E点和A点坐标,消去y得x2+x﹣2=0,然后解方程求出x即可得到E点的横坐标,从而得到点E到y轴的距离;(3)作QA⊥x轴于A,PB⊥x轴于B,如图,当a=1时,y=(x+2)2 , 则抛物线C1的顶点坐标为(﹣2,0),利用抛物线的几何变换得到抛物线C2的解析式为y=(x﹣1)2﹣2,即y=x2﹣2x﹣1,F(1,0),利用抛物线的对称性得FM=FN,再利用三角形面积公式可得QA=2PB,利用平行线分线段成比例定理得FA=2BF,设P(t,t2﹣2t﹣1),则BF=t﹣1,AF=2(t﹣1),则OA=2(t﹣1)﹣1=2t﹣3,所以Q[3﹣2t,(3﹣2t)2﹣2(3﹣2t)﹣1],然后利用AQ=2PB得到(3﹣2t)2﹣2(3﹣2t)﹣1=﹣2(t2﹣2t﹣1),解得t1=0(舍去),t2=2,于是得到P(2,﹣1),Q(﹣1,2),最后利用待定系数法确定直线l的解析式.
可得E点和A点坐标,消去y得x2+x﹣2=0,然后解方程求出x即可得到E点的横坐标,从而得到点E到y轴的距离;(3)作QA⊥x轴于A,PB⊥x轴于B,如图,当a=1时,y=(x+2)2 , 则抛物线C1的顶点坐标为(﹣2,0),利用抛物线的几何变换得到抛物线C2的解析式为y=(x﹣1)2﹣2,即y=x2﹣2x﹣1,F(1,0),利用抛物线的对称性得FM=FN,再利用三角形面积公式可得QA=2PB,利用平行线分线段成比例定理得FA=2BF,设P(t,t2﹣2t﹣1),则BF=t﹣1,AF=2(t﹣1),则OA=2(t﹣1)﹣1=2t﹣3,所以Q[3﹣2t,(3﹣2t)2﹣2(3﹣2t)﹣1],然后利用AQ=2PB得到(3﹣2t)2﹣2(3﹣2t)﹣1=﹣2(t2﹣2t﹣1),解得t1=0(舍去),t2=2,于是得到P(2,﹣1),Q(﹣1,2),最后利用待定系数法确定直线l的解析式.
【考点精析】本题主要考查了二次函数的图象的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的周长为38,第一条边长为a,第二条边比第一条边的2倍多3.
(1)表示第三条边;
(2)若三角形为等腰三角形,求a的值;
(3)若a为正整数,此三角形是否为直角三角形?说明理由.
-
科目: 来源: 题型:
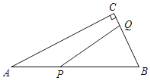
查看答案和解析>>【题目】已知,如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=18cm.动点P从点A出发,沿AB向点B运动,动点Q从点B出发,沿BC向点C运动,如果动点P以2cm/s,Q以1cm/s的速度同时出发,设运动时间为t(s),解答下列问题:
(1)t为何值时,△PBQ是等边三角形?
(2)P,Q在运动过程中,△PBQ的形状不断发生变化,当t为何值时,△PBQ是直角三角形?说明理由.
-
科目: 来源: 题型:
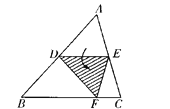
查看答案和解析>>【题目】如图,点D为边AB的中点,DE∥BC,将△ABC沿线段DE折叠,使点A落在点F处,若∠B=50°,则∠EDF=_______,∠BDF=_______,若AB=10cm,则FD= ________cm。
-
科目: 来源: 题型:
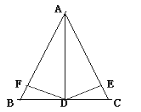
查看答案和解析>>【题目】如图:在△ABC中,AD是∠BAC的平分线,DE⊥AC于E,DF⊥AB于F,且FB=CE,则下列结论:①DE=DF,②AE=AF,③BD=CD,④AD⊥BC。
其中正确的有___________ (填序号)。
-
科目: 来源: 题型:
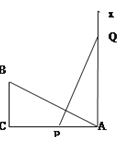
查看答案和解析>>【题目】如图,∠C=90°,AC=8,BC=3,线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到AP=_________时,才能使ΔABC与ΔAPQ 全等。
-
科目: 来源: 题型:
查看答案和解析>>【题目】作图题
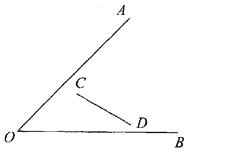
(1)如图:已知∠AOB和线段CD,求作一点P,使PC=PD,并且点P到∠AOB的两边距离相等(尺规作图,不写作法,保留作图痕迹,写出结论);
(2)如图:在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
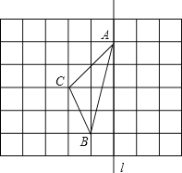
①在图中画出与关于直线
 成轴对称的△A′B′C′;
成轴对称的△A′B′C′;②线段CC′被直线
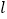 _________;
_________;③△ABC的面积为_________;
④在直线
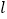 上找一点P,使PB+PC的长最短.
上找一点P,使PB+PC的长最短.
相关试题

