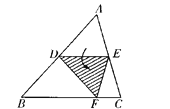
【题目】如图,点D为边AB的中点,DE∥BC,将△ABC沿线段DE折叠,使点A落在点F处,若∠B=50°,则∠EDF=_______,∠BDF=_______,若AB=10cm,则FD= ________cm。
参考答案:
【答案】50°80°5
【解析】
根据过三角形一边的中点且平行于另一边的直线必平分第三边可得E是AC的中点,进而得到DE是△ABC的中位线,DE∥BC,再根据两直线平行,同位角相等可得∠ADE=∠B ,根据翻折变换的性质可得∠ADE=∠EDF ,然后根据平角等于180°列式计算即可得解;根据线段中点的定义求出AD,再根据翻折的性质可得FD=AD.
点D为边AB的中点, DE∥BC,
∴E是AC的中点,
∴DE是△ABC的中位线,
∵DE∥BC,
∴∠ADE=∠B=50°,
由翻折的性质得, ∠ADE=∠EDF=50°,
∴∠BDF=180°-∠ADE-∠EDF=180°-50°-50°=80°,
∵AB=10cm,点D是AB的中点,
∴AD=![]() AB=
AB=![]() ×10=5cm,
×10=5cm,
由翻折的性质得,FD=AD=5cm.
故答案为:50°,80°,5.
-
科目: 来源: 题型:
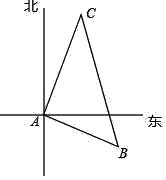
查看答案和解析>>【题目】如图,有一艘货船和一艘客船同时从港口A出发,客船每小时比货船多走5海里,客船与货船速度的比为4:3,货船沿东偏南10°方向航行,2小时后货船到达B处,客船到达C处,若此时两船相距50海里.
(1)求两船的速度分别是多少?
(2)求客船航行的方向.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的周长为38,第一条边长为a,第二条边比第一条边的2倍多3.
(1)表示第三条边;
(2)若三角形为等腰三角形,求a的值;
(3)若a为正整数,此三角形是否为直角三角形?说明理由.
-
科目: 来源: 题型:
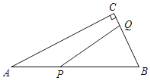
查看答案和解析>>【题目】已知,如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=18cm.动点P从点A出发,沿AB向点B运动,动点Q从点B出发,沿BC向点C运动,如果动点P以2cm/s,Q以1cm/s的速度同时出发,设运动时间为t(s),解答下列问题:
(1)t为何值时,△PBQ是等边三角形?
(2)P,Q在运动过程中,△PBQ的形状不断发生变化,当t为何值时,△PBQ是直角三角形?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,抛物线C1:y=ax2+4x+4a(0<a<2)

(1)当C1与x轴有唯一一个交点时,求此时C1的解析式;
(2)如图①,若A(1,yA),B(0,yB),C(﹣1,yC)三点均在C1上,连BC作AE∥BC交抛物线C1于E,求点E到y轴的距离;
(3)若a=1,将抛物线C1先向右平移3个单位,再向下平移2个单位得到抛物线C2 , 如图②,抛物线C2与x轴相交于点M、N(M点在N点的左边),抛物线的对称轴交x轴于点F,过点F的直线l与抛物线C2相交于P,Q(P在第四象限)且S△FMQ=2S△FNP , 求直线l的解析式. -
科目: 来源: 题型:
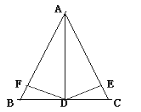
查看答案和解析>>【题目】如图:在△ABC中,AD是∠BAC的平分线,DE⊥AC于E,DF⊥AB于F,且FB=CE,则下列结论:①DE=DF,②AE=AF,③BD=CD,④AD⊥BC。
其中正确的有___________ (填序号)。
-
科目: 来源: 题型:
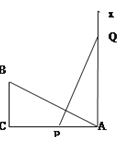
查看答案和解析>>【题目】如图,∠C=90°,AC=8,BC=3,线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到AP=_________时,才能使ΔABC与ΔAPQ 全等。
相关试题

