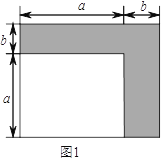
【题目】数学课上,我们知道可以用图形的面积来解释一些代数恒等式,如图![]() 可以解释完全平方公式:
可以解释完全平方公式:![]() .
.
(![]() )如图
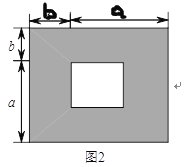
)如图![]() (图中各小长方形大小均相等),请用两种不同的方法求图
(图中各小长方形大小均相等),请用两种不同的方法求图![]() 中阴影部分的面积(不化简):
中阴影部分的面积(不化简):
方法![]() :______________________.
:______________________.
方法![]() :______________________.
:______________________.
(![]() )由(
)由(![]() )中两种不同的方法,你能得到怎样的等式?请说明这个等式成立;
)中两种不同的方法,你能得到怎样的等式?请说明这个等式成立;
(![]() )已知
)已知![]() ,
,![]() ,请利用(
,请利用(![]() )中的等式,求
)中的等式,求![]() 的值.
的值.
参考答案:
【答案】 (1). ![]() ,
, ![]() ;(2)见解析;(3)1.
;(2)见解析;(3)1.
【解析】
(1)根据阴影部分的面积=4个小长方形的面积=大正方形的面积-小正方形的面积,利用完全平方公式,即可解答; (2)根据完全平方公式解答; (3)根据平方差公式解答.
(![]() )
)![]() ;
;![]() .
.
(![]() )
)![]() ,成立.
,成立.
证:∵![]() .
.
![]() .
.
![]() .
.
∴得证
(![]() )
)![]() .
.
∴![]() .
.
![]() .
.
-
科目: 来源: 题型:
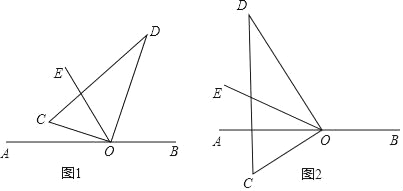
查看答案和解析>>【题目】如图,直角三角板的直角顶点O在直线AB上,OC,OD是三角板的两条直角边,OE平分∠AOD.
(1)若∠COE=20°,则∠BOD= ;若∠COE=α,则∠BOD= (用含α的代数式表示)
(2)当三角板绕O逆时针旋转到图2的位置时,其它条件不变,试猜测∠COE与∠BOD之间有怎样的数量关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个图形中,是中心对称图形的为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
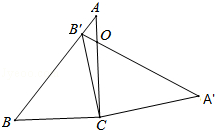
查看答案和解析>>【题目】如图,在三角形ABC中,∠ACB=90°,∠B=50°,将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C,若点B′恰好落在线段AB上,AC、A′B′交于点O,则∠COA′的度数是( )
A.50°
B.60°
C.70°
D.80° -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,直线
 ,另一直线交
,另一直线交 于
于 ,交
,交 于
于 ,且
,且 ,点
,点 为直线
为直线 上一动点,点
上一动点,点 为直线
为直线 上一动点,且
上一动点,且 .
.(
 )如图
)如图 ,当点
,当点 在点
在点 右边且点
右边且点 在点
在点 左边时,
左边时, 的平分线交
的平分线交 的平分线于点
的平分线于点 ,求
,求 的度数;
的度数;(
 )如图
)如图 ,当点
,当点 在点
在点 右边且点
右边且点 在点
在点 右边时,
右边时, 的平分线交
的平分线交 的平分线于点
的平分线于点 ,求
,求 的度数;
的度数;(
 )当点
)当点 在点
在点 左边且点
左边且点 在点
在点 左边时,
左边时, 的平分线交
的平分线交 的平分线所在直线交于点
的平分线所在直线交于点 ,请直接写出
,请直接写出 的度数,不说明理由.
的度数,不说明理由.


-
科目: 来源: 题型:
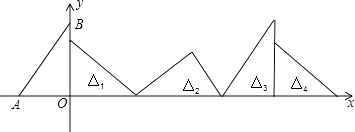
查看答案和解析>>【题目】如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2016的直角坐标顶点的坐标为( )
A.(8053,0)
B.(8064,0)
C.(8053,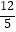 )
)
D.(8064,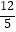 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解并完成下面问题:
我们知道,任意一个正整数
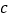 都可以进行这样的因式分解:
都可以进行这样的因式分解: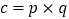 (
( 是正整数),在
是正整数),在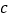 的所有这种分解中,如果
的所有这种分解中,如果 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称 是
是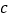 的最佳分解.并规定:
的最佳分解.并规定: (其中
(其中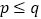 ).例如:
).例如: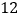 可以分解成
可以分解成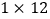 ,
, 或
或 ,因为
,因为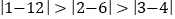 ,所以
,所以 是
是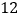 的最佳分解,所以
的最佳分解,所以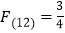 .
.(
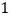 )如果一个正整数
)如果一个正整数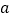 是另外一个正整数
是另外一个正整数 的平方,我们称正整数
的平方,我们称正整数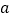 是完全平方数,若
是完全平方数,若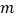 是一个完全平方数,求
是一个完全平方数,求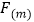 的值;
的值;(
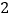 )如果一个两位正整数
)如果一个两位正整数 ,交换其个位数字与十位数字得到的新两位数减去原数所得的差为
,交换其个位数字与十位数字得到的新两位数减去原数所得的差为 ,那么我们称这个两位正整数
,那么我们称这个两位正整数 为“吉祥数”,求符合条件的所有“吉祥数”;
为“吉祥数”,求符合条件的所有“吉祥数”;(
 )在(
)在(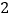 )中的所有“吉祥数”中,求
)中的所有“吉祥数”中,求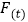 的最小值.
的最小值.
相关试题

