【题目】阅读理解并完成下面问题:
我们知道,任意一个正整数![]() 都可以进行这样的因式分解:
都可以进行这样的因式分解:![]() (
(![]() 是正整数),在
是正整数),在![]() 的所有这种分解中,如果
的所有这种分解中,如果![]() 两因数之差的绝对值最小,我们就称
两因数之差的绝对值最小,我们就称![]() 是
是![]() 的最佳分解.并规定:
的最佳分解.并规定:
![]() (其中
(其中![]() ).例如:
).例如:![]() 可以分解成
可以分解成![]() ,
,![]() 或
或![]() ,因为
,因为![]() ,所以
,所以![]() 是
是![]() 的最佳分解,所以
的最佳分解,所以![]() .
.
(![]() )如果一个正整数
)如果一个正整数![]() 是另外一个正整数
是另外一个正整数![]() 的平方,我们称正整数
的平方,我们称正整数![]() 是完全平方数,若
是完全平方数,若![]() 是一个完全平方数,求
是一个完全平方数,求![]() 的值;
的值;
(![]() )如果一个两位正整数
)如果一个两位正整数![]() ,交换其个位数字与十位数字得到的新两位数减去原数所得的差为
,交换其个位数字与十位数字得到的新两位数减去原数所得的差为![]() ,那么我们称这个两位正整数
,那么我们称这个两位正整数![]() 为“吉祥数”,求符合条件的所有“吉祥数”;
为“吉祥数”,求符合条件的所有“吉祥数”;
(![]() )在(
)在(![]() )中的所有“吉祥数”中,求
)中的所有“吉祥数”中,求![]() 的最小值.
的最小值.
参考答案:
【答案】(1)1;(2)![]() 可取
可取![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;(3)
;(3)![]()
【解析】(1)对任意一个完全平方数m,设m=n2(n为正整数),找出m的最佳分解,确定出F(m)的值即可;
(2)设交换t的个位上数与十位上的数得到的新数为t′,则t′=10y+x,根据“吉祥数”的定义确定出x与y的关系式,进而求出所求即可;
(3)利用“吉祥数”的定义分别求出各自的值,进而确定出F(t)的最小值即可.
(![]() )∵
)∵![]() 是完全平方数
是完全平方数
∴![]() 且
且![]()
∴![]()
(![]() )设正整数,则
)设正整数,则![]() ,则
,则![]() .
.
∵![]() .
.
![]() .
.
![]() .
.
∴![]() 可取
可取![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(![]() )由(
)由(![]() )得.
)得.
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
∵![]() .
.
∴![]() 的最小值为
的最小值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,我们知道可以用图形的面积来解释一些代数恒等式,如图
 可以解释完全平方公式:
可以解释完全平方公式: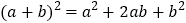 .
.(
 )如图
)如图 (图中各小长方形大小均相等),请用两种不同的方法求图
(图中各小长方形大小均相等),请用两种不同的方法求图 中阴影部分的面积(不化简):
中阴影部分的面积(不化简):方法
 :______________________.
:______________________.方法
 :______________________.
:______________________.(
 )由(
)由(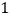 )中两种不同的方法,你能得到怎样的等式?请说明这个等式成立;
)中两种不同的方法,你能得到怎样的等式?请说明这个等式成立;(
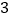 )已知
)已知 ,
,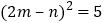 ,请利用(
,请利用( )中的等式,求
)中的等式,求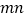 的值.
的值.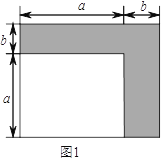
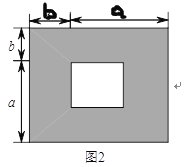
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,直线
 ,另一直线交
,另一直线交 于
于 ,交
,交 于
于 ,且
,且 ,点
,点 为直线
为直线 上一动点,点
上一动点,点 为直线
为直线 上一动点,且
上一动点,且 .
.(
 )如图
)如图 ,当点
,当点 在点
在点 右边且点
右边且点 在点
在点 左边时,
左边时, 的平分线交
的平分线交 的平分线于点
的平分线于点 ,求
,求 的度数;
的度数;(
 )如图
)如图 ,当点
,当点 在点
在点 右边且点
右边且点 在点
在点 右边时,
右边时, 的平分线交
的平分线交 的平分线于点
的平分线于点 ,求
,求 的度数;
的度数;(
 )当点
)当点 在点
在点 左边且点
左边且点 在点
在点 左边时,
左边时, 的平分线交
的平分线交 的平分线所在直线交于点
的平分线所在直线交于点 ,请直接写出
,请直接写出 的度数,不说明理由.
的度数,不说明理由.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2016的直角坐标顶点的坐标为( )
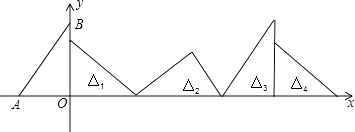
A.(8053,0)
B.(8064,0)
C.(8053,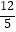 )
)
D.(8064,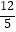 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
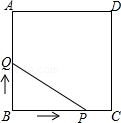
A.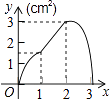
B.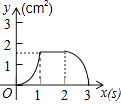
C.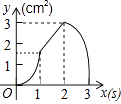
D.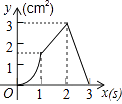
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在暑假社会实践活动中,以每千克
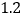 元的价格从批发市场购进若干千克西瓜市场上去销售,在销售了
元的价格从批发市场购进若干千克西瓜市场上去销售,在销售了 千克之后,余下的打折全部售完.销售金额
千克之后,余下的打折全部售完.销售金额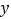 (元)售出西瓜的千克数
(元)售出西瓜的千克数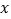 (千克)之间的关系如图所示.请你根据图像提供的信息完成以下问题:
(千克)之间的关系如图所示.请你根据图像提供的信息完成以下问题:(
 )求降价前销售金额
)求降价前销售金额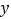 (元)与售出西瓜
(元)与售出西瓜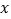 (千克)之间的关系;
(千克)之间的关系;(
 )小明这次社会实践活动赚了多少钱?
)小明这次社会实践活动赚了多少钱?(
 )若要使这次活动赚
)若要使这次活动赚 元钱,问余下的西瓜应打几折销售完?
元钱,问余下的西瓜应打几折销售完?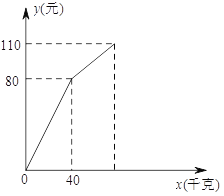
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式
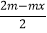 >
> x﹣1.
x﹣1.(1)当m=1时,求该不等式的解集;
(2)m取何值时,该不等式有解,并求出解集.
相关试题

