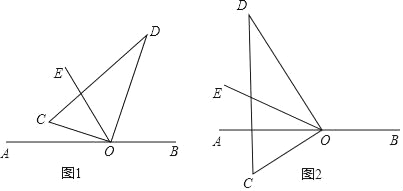
【题目】如图,直角三角板的直角顶点O在直线AB上,OC,OD是三角板的两条直角边,OE平分∠AOD.
(1)若∠COE=20°,则∠BOD= ;若∠COE=α,则∠BOD= (用含α的代数式表示)
(2)当三角板绕O逆时针旋转到图2的位置时,其它条件不变,试猜测∠COE与∠BOD之间有怎样的数量关系?并说明理由.
参考答案:
【答案】(1)40°;2α;(2)∠BOD=2∠COE.
【解析】试题分析:(1)先根据直角计算∠DOE的度数,再同角平分线的定义计算∠AOD的度数,最后利用平角的定义可得结论;
(2)设∠BOD=β,则∠AOD=180°-β,根据角平分线的定义表示∠BOE,再利用互余的关系求∠COE的度数,可得结论.
试题解析:(1)若∠COE=20°,
∵∠COD=90°,
∴∠EOD=90°﹣20°=70°,
∵OE平分∠AOD,
∴∠AOD=2∠EOD=140°,
∴∠BOD=180°﹣140°=40°;
若∠COE=α,
∴∠EOD=90﹣α,
∵OE平分∠AOD,
∴∠AOD=2∠EOD=2(90﹣α)=180﹣2α,
∴∠BOD=180°﹣(180﹣2α)=2α;
故答案为:40°;2α;
(2)如图2,∠BOD=2∠COE,理由是:
设∠BOD=β,则∠AOD=180°﹣β,
∵OE平分∠AOD,
∴∠EOD=![]() ∠AOD=
∠AOD=![]() =90°﹣
=90°﹣![]() ,
,
∵∠COD=90°,
∴∠COE=90°﹣(90°﹣![]() )=
)=![]() ,
,
即∠BOD=2∠COE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列实数中是无理数的是( )
A.
B.tan30°
C.3.14
D.2﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】在弹性限度内,弹簧挂上物体后会伸长,测得弹簧的长度
 与所挂物体的质量
与所挂物体的质量 之间有如下表关系:
之间有如下表关系:





…






…
下列说法不正确的是( )
A.
 随
随 的增大而增大 B. 所挂物体质量每增加
的增大而增大 B. 所挂物体质量每增加 弹簧长度增加
弹簧长度增加
C. 所挂物体为
 时,弹簧长度为
时,弹簧长度为 D. 不挂重物时弹簧的长度为
D. 不挂重物时弹簧的长度为
-
科目: 来源: 题型:
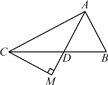
查看答案和解析>>【题目】如图,在△ABC中,AD是∠BAC的平分线,且∠B=∠ADB,过点C作CM垂直于AD的延长线,垂足为M.
(1)若∠DCM=α,试用α表示∠BAD;
(2)求证:AB+AC=2AM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个图形中,是中心对称图形的为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三角形ABC中,∠ACB=90°,∠B=50°,将此三角形绕点C沿顺时针方向旋转后得到三角形A′B′C,若点B′恰好落在线段AB上,AC、A′B′交于点O,则∠COA′的度数是( )
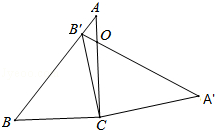
A.50°
B.60°
C.70°
D.80° -
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,我们知道可以用图形的面积来解释一些代数恒等式,如图
 可以解释完全平方公式:
可以解释完全平方公式: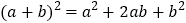 .
.(
 )如图
)如图 (图中各小长方形大小均相等),请用两种不同的方法求图
(图中各小长方形大小均相等),请用两种不同的方法求图 中阴影部分的面积(不化简):
中阴影部分的面积(不化简):方法
 :______________________.
:______________________.方法
 :______________________.
:______________________.(
 )由(
)由( )中两种不同的方法,你能得到怎样的等式?请说明这个等式成立;
)中两种不同的方法,你能得到怎样的等式?请说明这个等式成立;(
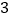 )已知
)已知 ,
,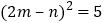 ,请利用(
,请利用( )中的等式,求
)中的等式,求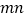 的值.
的值.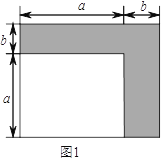
相关试题

